数据结构与算法

第一章（数据结构和算法）

数据结构

1. 官方定义-没有统一

解决问题的方法效率，跟数据的组织方式有关

空间的使用

解决问题的方法效率，跟空间的利用率有关
算法的效率

解决问题的方法效率，跟算法的巧妙程度有关
抽象数据类型

算法

1. 定义

1.一个有限指令集 （可行性）

2.接收一些输入 （有输入）

3.产生输出 （有输出）

4.在一定有限步骤后结束 （有穷性）

5.每一条指令必须有充分明确的目标，不可以有歧义，在计算机处理范围内，描述不依赖于任何一种计算机语言以及具体的实现手段 (确定性)

2. 算法的好坏

时间复杂度S（n）和空间复杂度T（n)

最坏情况复杂度T worst (n)

平均复杂度T avg (n)

Tworst(n)>=Tavg(n

3. 复杂度分析

复杂度分析的一些小窍门

T(n)是表示算法的时间复杂度。
O(n)是一种表示算法复杂度的符号,例如，T(n) = O(n^2)表示算法的时间复杂度为n的平方。
f(n)”在算法复杂度分析中通常用来表示函数关于输入规模n的增长率,f(n)”可以是一个具体的函数,也可以是一个泛指的函数。

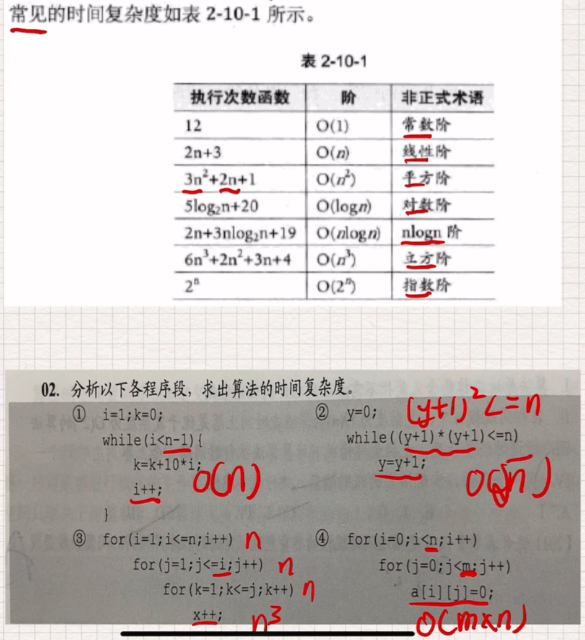
4. 时间复杂度计算

5. 算法的设计

1.正确性-没有语法错误

2.可读性-易读好交流

3.鲁棒性-抵抗非法输入的能力

4.高效性-时间效率和空间效率高

第二章(线性表堆栈队列)

线性表

线性表基本操作：插入，删除，查找

1. 多项式表示

顺序储存结构直接表示
顺序储存结构表示非零项

每个多项式可以看成系数和指数二元组的集合
链式结构储存非零项

链表中每个节点储存一个非零项，每个节点包括两个数据域和一个指针域

coef expon link

系数指数 next，指向下一个结构

coef	expon	link
系数	指数	next，指向下一个结构

// 多项式结点的指针类型，用于表示一个多项式
typedef struct PolyNode *Polynomial;
// 多项式结点的定义
struct PolyNode
{
	int cofe;           // 系数（coefficient）：表示项的常数系数
	int expon;          // 指数（exponent）：表示项的幂次
	Polynomial link;    // 指向下一个项的指针（用于构建链表结构）
};

链表的储存形式为：

2. 线性表顺序储存

线性表是由同类型数据元素构成有序序列的线性集合

表中元素个数成为线性表的长度
表中若无元素，称之为空表
表中的起始位置称为表头，结束位置称为表尾

线性表的抽象数据类型描述

线性表利用数组连续存储空间的顺序存放线性表的各元素

// 定义一个名为 List 的指向结构体 LNode 的指针类型
typedef struct LNode* List;
// 定义结构体 LNode，表示线性表
struct LNode
{
    ElementType Data[Maxsize]; // ElementType 可以是任何你想存储的数据类型
    int Last; // Last 表示线性表的最后一个元素的索引
};
// 声明一个结构体 LNode 类型的变量 L，用于创建线性表
struct LNode L;
// 声明一个 List 类型的指针变量 Ptrl，用于指向线性表的头节点
List Ptrl;

初始化

// 函数名：MakeEmpty
// 功能：创建一个空的线性表，并返回指向线性表头节点的指针
// 返回值：返回指向线性表头节点的指针 List
List MakeEmpty()
{
    List PtrL; // 声明一个 List 类型的指针变量 PtrL，用于指向线性表的头节点
    // 使用 malloc 分配内存来创建一个新的线性表头节点，并将其地址赋值给 PtrL
    PtrL = (List)malloc(sizeof(struct LNode));
    // 初始化线性表，将 Last 设置为 -1，表示当前线性表为空
    PtrL->Last = -1;
    // 返回指向新创建线性表头节点的指针
    return PtrL;
}

查找

// 函数名：Find
// 功能：在线性表 PtrL 中查找元素 X 的位置
// 参数：
//   - ElementType X: 要查找的元素
//   - List PtrL: 指向线性表头节点的指针
// 返回值：
//   - 成功找到元素 X 返回其在线性表中的位置（索引），从 0 开始
//   - 没有找到元素 X 返回 -1
int Find(ElementType X, List PtrL)
{
    int i = 0; // 初始化计数器 i，用于遍历线性表中的元素
    // 循环遍历线性表，查找元素 X
    while (i <= PtrL->Last && PtrL->Data[i] != X)
        i++;
    // 若找到元素 X，则返回其在线性表中的位置（索引）
    if (i > PtrL->Last)
        return -1; // 没有找到元素 X，返回 -1
    else
        return i;  // 成功找到元素 X，返回其位置（索引）
}

3. 顺序储存的插入和删除

插入（在i的位置上插入一个值为X的元素（1<=i<=n+1)

先移动再插入

// 函数名：Insert
// 功能：向线性表 PtrL 中的第 i 个位置插入元素 X
// 参数：
//   - ElementType X: 要插入的元素
//   - int i: 要插入的位置（索引），从 1 开始
//   - List PtrL: 指向线性表头节点的指针
// 返回值：无
void Insert(ElementType X, int i, List PtrL)
{
    int j; // 定义临时变量 j，用于循环中的计数
    // 判断线性表是否已满，如果已满则无法插入元素
    if (PtrL->Last == MAXSIZE - 1)//通过比较线性表的最后一个元素索引 Last 和线性表的最大容量 MAXSIZE-1 来判断线性表是否已满。
    {
        printf("该表已满");
        return;
    }
    // 判断插入位置 i 是否合法
    if (i >= PtrL->Last + 2 || i < 1)//检查插入位置 i 是否合法，不能超过当前线性表长度加 1，且不能小于 1。
    {
        printf("位置不合法");
        return;
    }
    // 从后往前遍历线性表，将第 i 个位置及其后的元素都往后移动一个位置
    for (j = PtrL->Last; j >= i - 1; j--)
    {
        PtrL->Data[j + 1] = PtrL->Data[j];
    }
    // 将元素 X 插入到第 i 个位置
    // 注意：由于数组下标从 0 开始，而 i 从 1 开始计数，所以插入位置应为 i-1
    PtrL->Data[i - 1] = X;
    // 更新线性表的最后一个元素的索引，将 Last 加 1，使其指向最后一个元素
    PtrL->Last++;
}

删除操作(删除第i个元素）
后面元素依次向前移动

// 函数名：Delete
// 功能：删除线性表 PtrL 中的第 i 个位置上的元素
// 参数：
//   - int i: 要删除的位置（索引），从 1 开始
//   - List PtrL: 指向线性表头节点的指针
// 返回值：无
void Delete(int i, List PtrL)
{
    int j; // 定义临时变量 j，用于循环中的计数
    // 检查插入位置 i 是否合法
    if (i >= PtrL->Last + 2 || i < 1)
    {
        printf("不存在第%d个元素", i);
        return;
    }
    // 从第 i 个位置开始，将后面的元素依次往前移动一个位置
    for (j = i; j <= PtrL->Last; j++)
    {
        PtrL->Data[j - 1] = PtrL->Data[j];
    }
    // 更新线性表的最后一个元素的索引，将 Last 减 1，表示删除了一个元素
    PtrL->Last--;
    return;
}

4. 链式储存和查找

链式储存解决了线性整体移动的问题，不要求逻辑上相邻的两个元素物理上也相邻，通过链建立数据元素之间的逻辑关系

插入删除不需要移动数据元素，只需要修改“链”

// 定义指向结构体 LNode 的指针类型 List
typedef struct LNode *List;
// 定义结构体 LNode，表示链表节点
struct LNode
{
	ElementType Data; // 存储节点的数据，ElementType 可以是任何你希望存储的数据类型
	List Next; // 指向下一个节点的指针
};
// 声明一个结构体 LNode 类型的变量 L，用于创建链表的头节点
struct LNode L;
// 声明一个 List 类型的指针变量 PtrL，用于指向链表的头节点
List PtrL;

求表长

// 函数名：Length
// 功能：计算链表 PtrL 的长度（节点个数）
// 参数：
//   - List PtrL: 指向链表头节点的指针
// 返回值：链表的长度（节点个数）
int Length(List PtrL)
{
	// 令 p 指向表的第一个节点，即头节点之后的第一个实际节点
	List p = PtrL->Next;

	int j = 0; // 初始化计数器 j，用于记录节点个数
	// 循环遍历链表，直到到达链表的结尾
	while (p)
	{
		p = p->Next; // 移动到下一个节点
		j++; // 计数器 j 自增，记录节点个数
	}
	return j; // 返回计数器 j，即为链表的长度
}

查找

按序号查找

// 函数名：Findkth
// 功能：在链表 PtrL 中查找第 k 个节点
// 参数：
//   - int k: 要查找的节点位置（索引），从 1 开始计数
//   - List PtrL: 指向链表头节点的指针
// 返回值：
//   - 如果找到第 k 个节点，返回指向该节点的指针
//   - 如果没有找到第 k 个节点或链表为空，返回 NULL
List Findkth(int k, List PtrL)
{
	List p = PtrL; // 令 p 指向链表的头节点
	int i = 1; // 初始化计数器 i，用于记录当前节点的位置（索引）
	// 循环遍历链表，查找第 k 个节点或链表的结尾
	while (p != NULL && i < k)
	{
		p = p->Next; // 移动到下一个节点
		i++; // 计数器 i 自增，记录当前节点的位置（索引）
	}
	// 如果找到第 k 个节点，则返回指向该节点的指针 p
	if (i == k)
		return p;
	else
		return NULL; // 没有找到第 k 个节点或链表为空，返回 NULL
}

按值查找

// 函数名：Find
// 功能：在链表 PtrL 中查找元素 X 的节点
// 参数：
//   - ElementType X: 要查找的元素
//   - List PtrL: 指向链表头节点的指针
// 返回值：
//   - 如果找到元素 X 的节点，返回指向该节点的指针
//   - 如果没有找到元素 X 或链表为空，返回 NULL
List Find(ElementType X, List PtrL)
{
    List p = PtrL; // 令 p 指向链表的头节点
    // 循环遍历链表，查找元素 X 的节点或链表的结尾
    while (p != NULL && p->Data != X)
        p = p->Next; // 移动到下一个节点
    // 如果找到元素 X 的节点，则返回指向该节点的指针 p
    // 如果没有找到元素 X 或链表为空，则返回 NULL
    return p;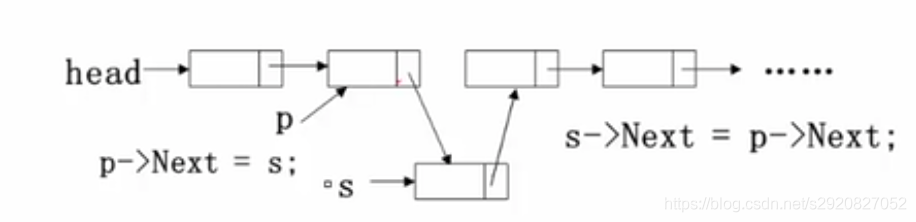
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

#### 5.  链式储存的插入和删除

- 插入操作（在第i个结点位置上插入一个值为X的新结点，换句话说就是在第i-1个结点后插入一个值为X的新节点）

  -  构造一个新结点用s指

  - 找到链表的第i-1个结点，用p指

  - 修改指针

    ```c
    // 函数名：Insert
    // 功能：向链表 PtrL 的第 i 个位置插入元素 X
    // 参数：
    //   - ElementType X: 要插入的元素
    //   - int i: 要插入的位置（索引），从 1 开始
    //   - List PtrL: 指向链表头节点的指针
    // 返回值：返回指向链表头节点的指针
    List Insert(ElementType X, int i, List PtrL)
    {
    	List p, s;
    	// 在链表头插入元素
    	if (i == 1)
    	{
    		// 申请一个新的节点 s
    		s = (List)malloc(sizeof(struct LNode));
    		s->Data = X;
    		s->Next = PtrL;
    		// 返回指向新头节点 s 的指针，即链表的新头指针
    		return s;
    	}
    	// 在其他位置插入元素
    	// 此处查找的节点为第 i-1 个节点
    	p = Findkth(i - 1, PtrL);
    	// 如果第 i-1 个节点不存在
    	if (p == NULL)
    	{
    		printf("参数出错");
    		return NULL;
    	}
    	else
    	{    // 申请一个新的节点 s
    		s = (List)malloc(sizeof(struct LNode));
    		s->Data = X;
    		// 将新节点 s 插入到第 i-1 个节点后面
    		s->Next = p->Next;
    		p->Next = s;
    		// 返回原链表的头指针 PtrL，表示链表没有改变头节点
    		return PtrL;
    	}
    }


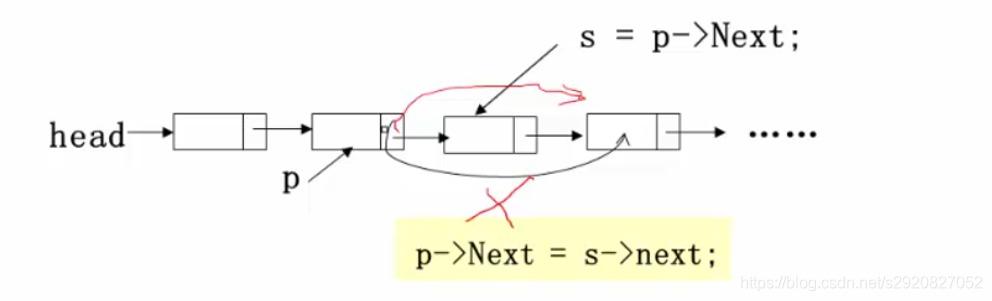
  ![](https://gcore.jsdelivr.net/gh/artly1/Image/202307171636241.png)

删除操作（删除第i个结点）（1<=i<=n)

先找到第i-1个结点，用p指向
然后用s指针指向第i个结点，即为p结点的下一个结点
修改指针，删除s所指向的结点
最后释放s所指向结点的空间free

// 函数名：Delete
// 功能：删除链表 PtrL 中的第 i 个节点
// 参数：
//   - int i: 要删除的节点位置（索引），从 1 开始
//   - List PtrL: 指向链表头节点的指针
// 返回值：返回指向链表头节点的指针
List Delete(int i, List PtrL)
{
	List p, s;
	// 删除头节点
	if (i == 1)
	{	
		s = PtrL;
		// 如果链表不为空，将头指针后移一位
		if (PtrL != NULL) 
			PtrL = PtrL->Next;
		else
			return NULL; // 链表为空，返回空指针
		free(s); // 释放原头节点的内存
		return PtrL;	// 返回新的头指针
	}
	// 删除其他位置的节点
	// 查找第 i-1 个节点，即要删除位置的前一个节点
	p = Findkth(i - 1, PtrL);
	// 如果第 i-1 个节点不存在
	if (p == NULL)
	{
		printf("第%d个结点不存在", i - 1);
		return NULL;
	}	
	else if (p->Next == NULL)
	{
		printf("第%d个结点不存在", i);
		return NULL;
	}
	else 
	{
		s = p->Next; // s 指向第 i 个节点
		p->Next = s->Next; // 删除操作，将第 i-1 个节点的指针域 Next 指向第 i+1 个节点
		free(s); // 释放第 i 个节点的内存
		return PtrL; // 返回原链表的头指针 PtrL
	}
}

6. 广义表和多重链表

一元多项式可以用上述式子表示，二元多项式又该如何表示？

广义表是线性表的推广
对于线性表来说，n个元素都是基本的单元素

广义表中，这些元素不仅是单元素也可以是另一个广义表

// 定义指向结构体 GNode 的指针类型 GList
typedef struct GNode *GList;
// 定义结构体 GNode，表示广义表的节点
struct GNode
{
	int Tag; // 标志域，0 表示结点是单元素，1 表示结点是广义表
	union//union：这是一个联合体，它是一种特殊的数据结构，允许在相同的内存位置存储不同类型的数据。在这里，union 中包含了两个成员：ElementType Data 和 GList Sublist。Data 用于存储单元素的数据，Sublist 用于存储子广义表的指针。
	{
		ElementType Data; // 数据域 Data，用于存储单元素数据
		GList Sublist; // 指针域 Sublist，用于存储子广义表的指针
	} URegion; // 联合体，数据域 Data 和指针域 Sublist 复用存储空间
	GList Next; // 指向后继结点的指针
};

多重链表
多重链表中的结点属于多个链
- 多重链表中的结点指针域有很多，
- 但是包含两个指针域的链表并不一定是多重链表，
- 比如双向链表不是多重链表
- 多重链表可以用在树和图中实现存储

堆栈

什么是堆栈?

堆栈是具有一定操作约束的线性表，只在一端做插入，删除
Last In First Out（LIFO）后入先出

中缀表达式：运算符位于两个数字之间
后缀表达式：运算符位于两个数字之后

抽象数据类型

原理图

堆栈的顺序存储
栈的顺序存储结构通常是由一个一维数组和一个记录栈顶元素位置的变量组成

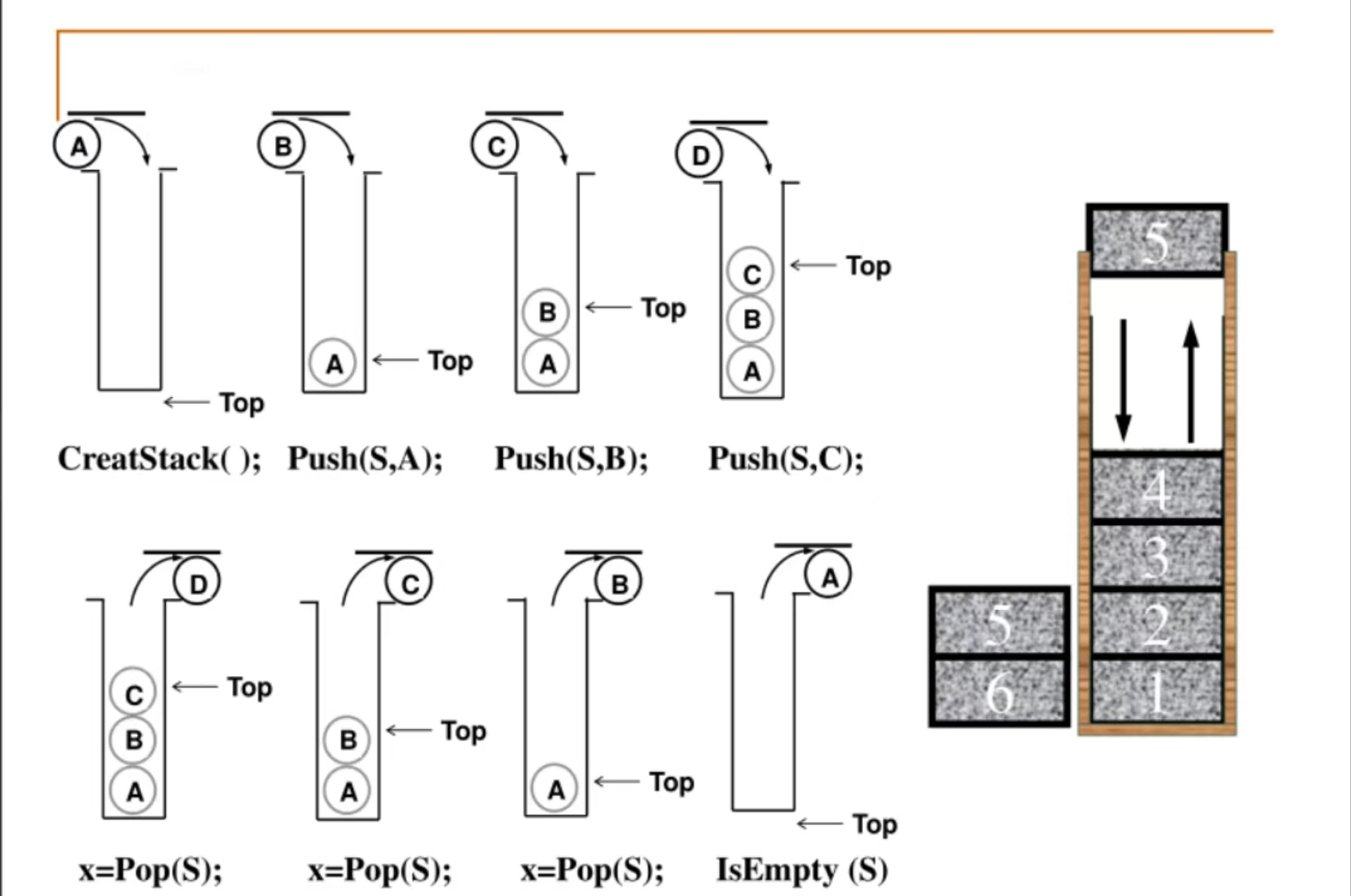
// 定义存储数据元素的最大值
#define Maxsize <存储数据元素的最大值>
// 定义指向结构体 SNode 的指针类型 Stack
typedef struct SNode *Stack;
// 定义结构体 SNode，表示栈
struct SNode
{
	ElementType Data[Maxsize]; // 用于存储数据元素的数组，数组大小为 Maxsize
	int Top; // 栈顶指针，表示栈顶元素在数组中的索引
};

入栈

// 函数名：Push
// 功能：将元素 item 入栈
// 参数：
//   - Stack PtrL: 指向栈的指针
//   - ElementType item: 要入栈的元素
// 返回值：无
void Push(Stack PtrL, ElementType item)
{
	// 检查栈是否已满
	if (PtrL->Top == Maxsize - 1)
	{
		printf("堆栈满"); // 输出错误信息，表示栈已满
		return;
	}
	else
	{
		PtrL->Data[++(PtrL->Top)] = item; // 将元素 item 入栈，栈顶指针 Top 自增
		return;
	}
}

出栈

// 函数名：Pop
// 功能：将栈顶元素出栈，并返回该元素的值
// 参数：
//   - Stack PtrL: 指向栈的指针
// 返回值：返回栈顶元素的值，如果栈为空，返回 ERROR（出错值）
ElementType Pop(Stack PtrL)
{
	// 检查栈是否为空
	if (PtrL->Top == -1)
	{
		printf("堆栈空"); // 输出错误信息，表示栈为空
		return ERROR; // 返回 ERROR（出错值）
	}
	else
	{
		return (PtrL->Data[(PtrL->Top)--]); // 将栈顶元素出栈，并返回该元素的值，栈顶指针 Top 自减
	}
}

用数组实现两个堆栈，最大利用数组空间，若有空间则可以实现入栈

两个栈分别从数组的两头开始向中间生长，当两个栈的栈顶指针相遇时，表示两个栈都已经满

// 定义存储数据元素的最大个数
#define MaxSize <存储数据元素的最大个数>

// 定义结构体 DoubleStack，表示双栈
struct DoubleStack {
	ElementType Data[MaxSize]; // 用于存储数据元素的数组，数组大小为 MaxSize
	int Top1; // 栈1的栈顶指针
	int Top2; // 栈2的栈顶指针
};
// 创建一个双栈 S，同时初始化栈1的栈顶指针 Top1 为 -1，栈2的栈顶指针 Top2 为 MaxSize
struct DoubleStack S;
S.Top1 = -1;
S.Top2 = MaxSize;

// 函数名：Push
// 功能：将元素 item 入栈
// 参数：
//   - struct DoubleStack *PtrS: 指向双栈的指针
//   - ElementType item: 要入栈的元素
//   - int Tag: 表示入栈到哪个栈，Tag=1 表示栈1，Tag=2 表示栈2
// 返回值：无
void Push(struct DoubleStack *PtrS, ElementType item, int Tag) {
	// 检查栈是否已满
	if (PtrS->Top2 - PtrS->Top1 == 1) {
		printf("堆栈满"); // 输出错误信息，表示双栈已满
		return;
	}

	// 判断入栈到哪个栈，Tag=1 表示栈1，Tag=2 表示栈2
	if (Tag == 1)
		PtrS->Data[++(PtrS->Top1)] = item; // 将元素 item 入栈到栈1，栈1的栈顶指针 Top1 自增
	else
		PtrS->Data[--(PtrS->Top2)] = item; // 将元素 item 入栈到栈2，栈2的栈顶指针 Top2 自减
}
// 函数名：Pop
// 功能：将栈顶元素出栈，并返回该元素的值
// 参数：
//   - struct DoubleStack *PtrS: 指向双栈的指针
//   - int Tag: 表示出栈哪个栈，Tag=1 表示栈1，Tag=2 表示栈2
// 返回值：返回栈顶元素的值，如果栈为空，返回 NULL（出错值）
ElementType Pop(struct DoubleStack *PtrS, int Tag) {
	// 判断出栈哪个栈，Tag=1 表示栈1，Tag=2 表示栈2
	if (Tag == 1) {
		// 检查栈1是否为空
		if (PtrS->Top1 == -1) {
			printf("堆栈1空"); // 输出错误信息，表示栈1为空
			return NULL; // 返回 NULL（出错值）
		} else
			return PtrS->Data[(PtrS->Top1)--]; // 将栈1的栈顶元素出栈，并返回该元素的值，栈1的栈顶指针 Top1 自减
	} else {
		// 检查栈2是否为空
		if (PtrS->Top2 == MaxSize) {
			printf("堆栈空"); // 输出错误信息，表示栈2为空
			return NULL; // 返回 NULL（出错值）
		} else
			return PtrS->Data[(PtrS->Top2)++]; // 将栈2的栈顶元素出栈，并返回该元素的值，栈2的栈顶指针 Top2 自增
	}
}

堆栈的链式存储

链式存储结构实际上就是一个单链表，叫做链栈，插入和删除操作只能在链栈的栈顶进行

// 定义指向结构体 SNode 的指针类型 Stack
typedef struct SNode *Stack;
// 定义结构体 SNode，表示栈节点
struct SNode 
{
	ElementType Data; // 数据域，用于存储栈节点的数据元素
	struct SNode *Next; // 指针域，指向下一个栈节点的指针
};

初始化

// 函数名：CreatStack
// 功能：创建一个空栈，并返回指向栈顶节点的指针
// 参数：无
// 返回值：返回指向栈顶节点的指针
Stack CreatStack()
{
	Stack s; // 声明一个指向栈节点的指针 s
	// 分配内存，创建一个栈节点
	s = (Stack)malloc(sizeof(struct SNode));
	// 初始化栈节点的指针域 Next 为 NULL，表示栈为空
	s->Next = NULL;
	return s; // 返回指向栈顶节点的指针
}

判断堆栈s是否为空

int Empty(Stack s)
{
	return (s->Next == NULL);
}

入栈

// 函数名：Push
// 功能：将元素 item 入栈
// 参数：
//   - ElementType item: 要入栈的元素
//   - Stack s: 指向栈顶节点的指针
// 返回值：无
void Push(ElementType item, Stack s)
{
	// 创建一个新的栈节点
	struct SNode *Tmpcell;
	Tmpcell = (struct SNode *)malloc(sizeof(struct SNode));
	// 设置新栈节点的数据域 Element 为要入栈的元素 item
	Tmpcell->Element = item;
	// 将新栈节点插入到栈顶节点之后
	Tmpcell->Next = s->Next;
	s->Next = Tmpcell;
}

出栈

// 函数名：Pop
// 功能：将栈顶元素出栈，并返回该元素的值
// 参数：
//   - Stack s: 指向栈顶节点的指针
// 返回值：返回栈顶元素的值，如果栈为空，返回 NULL（出错值）
ElementType Pop(Stack s)
{
	struct SNode *Firstcell; // 声明一个指向栈节点的指针 Firstcell，用于暂存要出栈的栈顶节点
	ElementType TopElement; // 声明一个变量 TopElement，用于存储要出栈的栈顶元素
	// 检查栈是否为空
	if (Empty(s))
	{
		printf("堆栈空"); // 输出错误信息，表示栈为空
		return NULL; // 返回 NULL（出错值）
	}
	else 
	{
		// 将栈顶节点出栈，注意保存要删除的元素和栈顶元素
		Firstcell = s->Next; // Firstcell 指向要删除的栈顶节点
		s->Next = Firstcell->Next; // 将栈顶指针 Next 指向删除节点的下一个节点，即出栈操作
		TopElement = Firstcell->Element; // 将要出栈的栈顶元素存储到 TopElement 中
		free(Firstcell); // 释放删除的节点的内存，即释放栈顶节点的内存
		return TopElement; // 返回栈顶元素的值
	}
}

堆栈的应用

中缀表达式转换为后缀表达式
运算数：直接输出
左括号：入栈
右括号：栈顶元素出栈并输出，直到遇到左括号
运算符：优先级大于栈顶运算符，入栈；优先级小于等于栈顶运算符出栈输出，继续比较新的栈顶运算符
处理完毕后，将堆栈剩余元素一并输出

队列

队列及顺序存储
具有一定操作约束的线性表

插入和删除操作：只能在一端插入，而在另一端删除
数据插入：入队列
数据删除：出队列
先进先出（FIFO）First In First Out
抽象数据描述

队列存储的实现

队列的顺序存储结构通常由一个一维数组和一个记录队列头元素位置的变量ront以及一个记录队列尾元素位置的变量rear组成

// 定义存储数据元素的最大个数
#define Maxsize <数据元素的最大个数>
// 定义队列结构体 QNode
struct QNode {
	ElementType Data[Maxsize]; // 用于存储数据元素的数组，数组大小为 Maxsize
	int rear; // 队尾指针，指向队列最后一个元素的下标
	int front; // 队首指针，指向队列第一个元素之前的位置
};
// 定义指向队列结构体 QNode 的指针类型 Queue
typedef struct QNode *Queue;
// front 指的是第一个元素之前的位置

在顺环队列判断是否满的问题上使用额外标记Tag域或者Size

入队

// 函数名：AddQ
// 功能：向队列尾部添加元素
// 参数：
//   - Queue PtrL: 指向队列的指针
//   - ElementType item: 要添加的元素
// 返回值：无
void AddQ(Queue PtrQ, ElementType item)
{
	// 检查队列是否已满
	if ((PtrQ->rear + 1) % Maxsize == PtrQ->front)
	{
		printf("队列满"); // 输出错误信息，表示队列已满
		return; // 返回，不执行入队操作
	}

	// 将队尾指针后移一位，考虑循环队列的情况
	PtrQ->rear = (PtrQ->rear + 1) % Maxsize;

出队

// 函数名：DQ
// 功能：从队列头部删除元素，并返回该元素的值
// 参数：
//   - Queue PtrQ: 指向队列的指针
// 返回值：返回队列头部元素的值，如果队列为空，返回 ERROR（出错值）
ElementType DQ(Queue PtrQ)
{
	// 检查队列是否为空
	if (PtrQ->rear == PtrQ->front)
	{
		printf("队列空"); // 输出错误信息，表示队列为空
		return ERROR; // 返回 ERROR（出错值）
	}
	else 
	{
		// 将队首指针后移一位，考虑循环队列的情况
		PtrQ->front = (PtrQ->front + 1) % Maxsize;
		// 返回队列头部元素的值
		return PtrQ->Data[PtrQ->front];
	}
}

队列的链式存储

// 定义链式队列节点结构体 Node
struct Node {
	ElementType Data;   // 数据域，用于存储节点的数据元素
	struct Node *Next;  // 指针域，指向下一个节点的指针
};
// 定义链式队列结构体 QNode
struct QNode {
	struct Node *rear;  // 队尾指针，指向队列中最后一个元素的节点
	struct Node *front; // 队首指针，指向队列中第一个元素的节点
};
// 定义指向链式队列结构体 QNode 的指针类型 Queue
typedef struct QNode *Queue;
// 声明一个指向链式队列结构体 QNode 的指针 PtrQ
Queue PtrQ;

出队

// 函数名：DQ
// 功能：从队列头部删除元素，并返回该元素的值
// 参数：
//   - Queue PtrQ: 指向链式队列的指针
// 返回值：返回队列头部元素的值，如果队列为空，返回 ERROR（出错值）

ElementType DQ(Queue PtrQ)
{
	struct Node *Frontcell; // 声明一个指向链式队列节点的指针 Frontcell，用于暂存要出队的节点
	ElementType Frontelement; // 声明一个变量 Frontelement，用于存储要出队的队列头部元素
	// 检查队列是否为空
	if (PtrQ->front == NULL)
	{
		printf("空"); // 输出错误信息，表示队列为空
		return ERROR; // 返回 ERROR（出错值）
	}
	// 将队首节点出队
	Frontcell = PtrQ->front; // Frontcell 指向要出队的队列头部节点
	// 分情况讨论，队列只有一个元素和多个元素
	if (PtrQ->front == PtrQ->rear)
		PtrQ->front = PtrQ->rear = NULL; // 如果队列只有一个元素，出队后将队首指针和队尾指针都设置为 NULL，表示队列为空
	else
		PtrQ->front = PtrQ->front->Next; // 如果队列有多个元素，将队首指针后移，即将第二个节点设置为队首节点

	Frontelement = Frontcell->Data; // 将要出队的队列头部元素存储到 Frontelement 中
	free(Frontcell); // 释放出队的节点的内存，即释放队列头部节点的内存
	return Frontelement; // 返回队列头部元素的值，表示成功出队
}

多项式问题

加法运算的实现

采用不带头结点的单项链表。按照指数递减的顺序排列各项

struct PolyNode{
	int coef;//系数
	int expon;//指数
	struct PolyNode *link;
};
typedef struct PolyNode *Polynomial;
Polynomial P1,P2;

算法思路
P1->expon==P2->expon:系数相加，若结果不为0，则作为结果多项式对应系数。同时，P1和P2 都指向下一项
P1->expon>P2->expon将P1存入当前多项式，并使P1指向下一项
P1->expon < P2->expon将P2存入当前多项式，并使P2指向下一项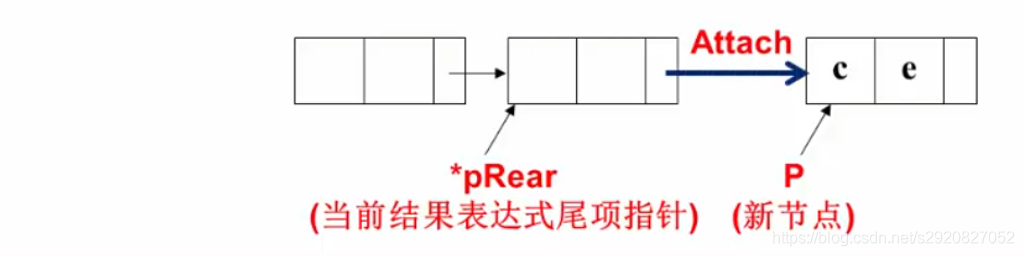

// 函数名：Polynomial Polyadd(Polynomial P1, Polynomial P2)
// 功能：多项式相加
// 参数：
//   - Polynomial P1: 第一个多项式的头结点指针
//   - Polynomial P2: 第二个多项式的头结点指针
// 返回值：返回多项式相加后的结果多项式的头结点指针
Polynomial Polyadd(Polynomial P1, Polynomial P2)
{
   Polynomial front, rear, temp;
   int sum;
   rear = (Polynomial)malloc(sizeof(struct PolyNode));
   front = rear;
   // front 这里指的是多项式链表头结点
   while (P1 && P2)
   {
      switch (Compare(P1->expon, P2->expon))
      {
         case 1:
            Attach(P1->coef, P1->expon, &rear);
            P1 = P1->link;
            break;
         case -1:
            Attach(P2->coef, P2->expon, &rear);
            P2 = P2->link;
            break;
         case 0:
            sum = P1->coef + P2->coef;
            if (sum) Attach(sum, P1->expon, &rear);
            P1 = P1->link;
            P2 = P2->link;
            break;
      }
   }
   // 还有未处理完的另一个多项式的所有结点依此复制
   for (; P1; P1 = P1->link) Attach(P1->coef, P1->expon, &rear);
   for (; P2; P2 = P2->link) Attach(P2->coef, P2->expon, &rear);
   
   rear->link = NULL; // 将链表最后一个节点的 next 指针置为 NULL，表示链表结束
   temp = front;
   front = front->link; // 头结点的下一个节点即为结果多项式的头结点
   free(temp); // 释放头结点的内存，防止内存泄漏
   return front; // 返回结果多项式的头结点指针
}
// 函数名：void Attach(int c, int e, Polynomial *pRear)
// 功能：将系数为 c，指数为 e 的节点添加到链表中
// 参数：
//   - int c: 系数值
//   - int e: 指数值
//   - Polynomial *pRear: 链表尾节点的指针的指针，用于更新链表尾节点
// 返回值：无
void Attach(int c, int e, Polynomial *pRear)
{
   Polynomial P;
   P = (Polynomial)malloc(sizeof(struct PolyNode));
   P->coef = c;
   P->expon = e;
   P->link = NULL;
   (*pRear)->link = P;
   *pRear = P;
   // 修改 pRear 值，使其指向链表尾部节点，以便下次添加节点时可以直接在尾部插入
}

题意理解与多项式表示

数据结构设计

// 定义多项式结点指针类型 Polynomial，是指向 struct PolyNode 结构体的指针
typedef struct PolyNode *Polynomial;
// 定义多项式结点结构体 PolyNode
struct PolyNode
{
	int coef;           // 系数，用于存储多项式项的系数值
	int expon;          // 指数，用于存储多项式项的指数值
	Polynomial link;    // 指向下一个多项式结点的指针，用于将多项式的各项连接在一起
};
// 这个代码片段定义了一个简单的链式存储结构用于表示多项式。
// 多项式的每一项包含两个部分：系数 coef 和指数 expon。
// 用链表将各项连接在一起，每个节点通过 link 指针指向下一个节点。
// 多项式的头结点可以用 Polynomial 类型的指针来表示，即指向第一个多项式节点的指针。

程序框架及读入多项式

// 函数名：main
// 功能：主函数，用于调用多项式相关函数
// 返回值：整数类型，表示程序的结束状态
int main()
{
	// 声明多项式 P1, P2, PP, PS
	Polynomial P1, P2, PP, PS;
	// 读入第一个多项式 P1
	P1 = ReadPoly();
	// 读入第二个多项式 P2
	P2 = ReadPoly();
	// 将两个多项式 P1 和 P2 相乘，结果存储在 PP 中
	PP = Mult(P1, P2);
	// 打印相乘结果多项式 PP
	PrintPoly(PP);
	// 将两个多项式 P1 和 P2 相加，结果存储在 PS 中
	PS = Add(P1, P2);
	// 打印相加结果多项式 PS
	PrintPoly(PS);
	return 0; // 返回程序的结束状态，表示成功执行
}

读取多项式

// 函数名：Polynomial ReadPoly()
// 功能：读取一个多项式，并以链表形式返回该多项式的头结点指针
// 返回值：多项式的头结点指针
Polynomial ReadPoly()
{
	// 声明多项式头结点指针 P, Rear 和临时指针 t
	Polynomial P, Rear, t;
	int c, e, N;
	// 从标准输入读取多项式的项数 N
	scanf("%d", &N);
	// 创建链表头空结点 P，Rear 指向头结点
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->link = NULL;
	Rear = P;
	// 依次读入 N 个多项式项，并将其插入链表尾部
	while (N--)
	{
		scanf("%d %d", &c, &e);
		Attach(c, e, &Rear);
		// 将当前项插入多项式尾部
	}
	// 删除临时生成的头结点，并将链表的真正头结点指针 P 返回
	t = P;
	P = P->link;
	free(t);
	return P;
}
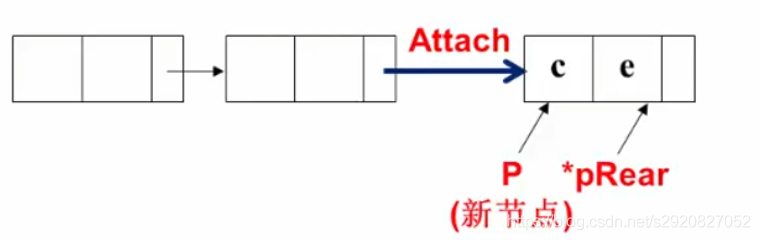
// 函数名：void Attach(int c, int e, Polynomial *pRear)
// 功能：将系数为 c，指数为 e 的节点添加到链表中
// 参数：
//   - int c: 系数值
//   - int e: 指数值
//   - Polynomial *pRear: 链表尾节点的指针的指针，用于更新链表尾节点
// 返回值：无
void Attach(int c, int e, Polynomial *pRear)
{
	// 创建新的多项式节点 P，并分别赋值系数和指数
	Polynomial P;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->coef = c;
	P->expon = e;
	P->link = NULL;
	// 将新节点 P 插入链表尾部，更新链表尾节点指针 pRear
	(*pRear)->link = P;
	*pRear = P;
}

加法乘法及多项式的输出

上面已经写过此代码

两个多项式相乘

// 函数名：Polynomial Mult(Polynomial P1, Polynomial P2)
// 功能：计算两个多项式 P1 和 P2 的乘积，结果以链表形式返回
// 参数：
//   - Polynomial P1: 第一个多项式的头结点指针
//   - Polynomial P2: 第二个多项式的头结点指针
// 返回值：多项式的头结点指针，表示乘积多项式
Polynomial Mult(Polynomial P1, Polynomial P2)
{
	// 声明多项式头结点指针 P, Rear 和临时指针 t1, t2, t
	Polynomial P, Rear, t1, t2, t;
	int c, e;
	// 如果 P1 或 P2 为空，则返回空指针
	if (!P1 || !P2) return NULL;
	// 复制 P1 的头结点，用于计算结果多项式 P
	t1 = P1;
	// 复制 P2 的头结点，用于遍历 P2
	t2 = P2;
	// 创建链表头空结点 P，Rear 指向头结点
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->link = NULL;
	Rear = P;
	// 第一重循环，计算 P1 的第一项和 P2 的每一项的乘积，插入到结果多项式 P 中
	while (t2)
	{
		// 将 P1 的第一项与 P2 的当前项相乘，并将结果插入到结果多项式 P 中
		Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
		// 将 P2 的指针 t2 后移，继续处理下一项
		t2 = t2->link;
	}
	// 将 P1 的指针 t1 后移，继续处理下一项
	t1 = t1->link;
	// 第二重循环，计算 P1 的每一项和 P2 的每一项的乘积，插入到结果多项式 P 中
	while (t1)
	{
		// 重新将 P2 的指针 t2 移回 P2 的头结点，并将 Rear 指针指向结果多项式 P 的头结点
		t2 = P2;
		Rear = P;
		// 遍历 P2，计算 P1 的当前项与 P2 的每一项的乘积，并插入到结果多项式 P 中
		while (t2)
		{
			// 计算当前项的指数和系数
			e = t1->expon + t2->expon;
			c = t1->coef * t2->coef;
			// 找到合适的位置插入或处理相等指数的情况
			while (Rear->link && Rear->link->expon > e)
				Rear = Rear->link;
			// 处理相等指数的情况，相同指数项的系数相加
			if (Rear->link && Rear->link->expon == e)
			{
				if (Rear->link->coef == c)
					Rear->link->coef += c;
				else
				{
					// 删除节点，系数为 0 的项
					t = Rear->link;
					Rear->link = t->link;
					free(t);
				}
			}
			// 不相等则申请新的结点并插入
			else
			{
				t = (Polynomial)malloc(sizeof(struct PolyNode));
				t->coef = c;
				t->expon = e;
				// 插入过程
				t->link = Rear->link;
				Rear->link = t;
				Rear = Rear->link;
			}
			t2 = t2->link;
		}
		// 处理完 P1 的一项，将指针后移，继续处理下一项
		t1 = t1->link;
	}
	// 删除临时生成的头结点，并将链表的真正头结点指针 P 返回
	t2 = P;
	P = P->link;
	free(t2);
	return P;
}

多项式输出

// 函数名：void PrintPoly(Polynomial P)
// 功能：打印多项式 P 的系数和指数
// 参数：
//   - Polynomial P: 多项式的头结点指针
// 返回值：无
void PrintPoly(Polynomial P)
{
	int flag = 0;
	// flag 用于调整输出格式，初始为 0
	// 如果多项式为空，则打印 "0 0" 表示零多项式，并直接返回
	if (!P)
	{
		printf("0 0\n");
		return;
	}
	// 遍历多项式链表并输出系数和指数
	while (P)
	{
		// 当 flag 为 0 时，输出第一项，不加空格；否则输出空格
		if (!flag)
			flag = 1;
		else
			printf(" ");
		// 输出当前多项式节点的系数和指数
		printf("%d %d", P->coef, P->expon);
		// 指针后移，处理下一项
		P = P->link;
	}
	// 打印完所有项后换行
	printf("\n");
}

第三章（树.上）

树与树的表示

顺序查找

查找：根据给定某个关键字K，从集合R中找出关键字与K相同的记录
静态查找：集合中记录是固定的，没有删除和插入操作只有查找操作

动态查找：集合中记录是动态的，除了查找操作，还可能有删除和插入操作`

// 定义一个指向结构体 LNode 的指针类型 List
typedef struct LNode* List;
// 定义结构体 LNode
struct LNode 
{
    // 数据域，用于存储元素的数组
    ElementType Element[Maxsize];
    // 当前线性表的长度
    int length;
};

有哨兵

// 在顺序表 Tb1 中进行顺序查找元素 K 的位置
// 参数：
//   - List Tb1: 顺序表的指针，表示要进行查找的顺序表
//   - ElementType K: 要查找的元素
// 返回值：
//   - 如果找到元素 K，返回其在顺序表 Tb1 中的位置；如果未找到，返回 -1。
int SequentialSearch(List Tb1, ElementType K)
{
    int i;
    // 将要查找的元素 K 放在顺序表 Tb1 的第一个位置，作为哨兵
    Tb1->Element[0] = K;
    // 从顺序表的末尾开始逆序遍历，查找元素 K 的位置
    for (i = Tb1->length; Tb1->Element[i] != K; i--);
    // 如果 i 等于 0，说明未找到元素 K，返回 -1
    // 否则返回找到的元素 K 在顺序表 Tb1 中的位置
    return i ;
}

无哨兵

// 在顺序表 Tb1 中进行顺序查找元素 K 的位置
// 参数：
//   - List Tb1: 顺序表的指针，表示要进行查找的顺序表
//   - ElementType K: 要查找的元素
// 返回值：
//   - 如果找到元素 K，返回其在顺序表 Tb1 中的位置；如果未找到，返回 -1。
int SequentialSearch(List Tb1, ElementType K)
{
    int i;
    // 从顺序表的末尾开始逆序遍历，查找元素 K 的位置
    for (i = Tb1->length; i > 0 && Tb1->Element[i] != K; i--);
    // 如果 i 等于 0，说明未找到元素 K，返回 -1
    // 否则返回找到的元素 K 在顺序表 Tb1 中的位置
    return i == 0 ? -1 : i;
}

二分查找（Binary Search）

要求：数组连续，有序
思路：利用mid，right，left三者的比较缩小范围，查找值
left>right?查找失败：结束;
复杂度：log（n）

// 在有序顺序表 Tb1 中进行二分查找元素 K 的位置
// 参数：
//   - List Tb1: 有序顺序表的指针，表示要进行查找的顺序表
//   - ElementType K: 要查找的元素
// 返回值：
//   - 如果找到元素 K，返回其在顺序表 Tb1 中的位置（数组下标）；如果未找到，返回 -1。
int BinarySearch(List Tb1, ElementType K)
{
    int mid, right, left, notFound = -1;
    left = 1;              // 左边界，初始为第一个元素位置
    right = Tb1->length;   // 右边界，初始为最后一个元素位置
    mid = (left + right) / 2; // 中间位置
    while (left <= right)
    {
        // 如果中间元素大于要查找的元素 K，说明要查找的元素在左半部分
        if (Tb1->Element[mid] > K)
            right = mid - 1;
        // 如果中间元素小于要查找的元素 K，说明要查找的元素在右半部分
        else if (Tb1->Element[mid] < K)
            left = mid + 1;
        // 查找成功，返回元素 K 的位置（数组下标）
        else
            return mid;
        // 更新中间位置
        mid = (left + right) / 2;
    }
    // 循环结束仍未找到，返回未找到标志 -1
    return notFound;
}

树的定义和表示

定义：树是由n（n>=0）个结点构成的有限集合
每一个树都有一个根结点（root），用r表示
其余结点可以分为数个互不相交的有限集合，每个集合又是一个树，称为原来树的子树
每颗树的子树互不相交，除了根结点外，每个结点只有一个父结点，每个有N个结点的树有N-1条边
树的一些基本术语：
- 结点的度：结点的子树个数。
- 树的度: 是所有结点中最大的度数。
- 节点的层次：规定根结点在一层，其他任一节点层次是其父结点的层次＋1
- 树的深度：树中所有结点的最大层次

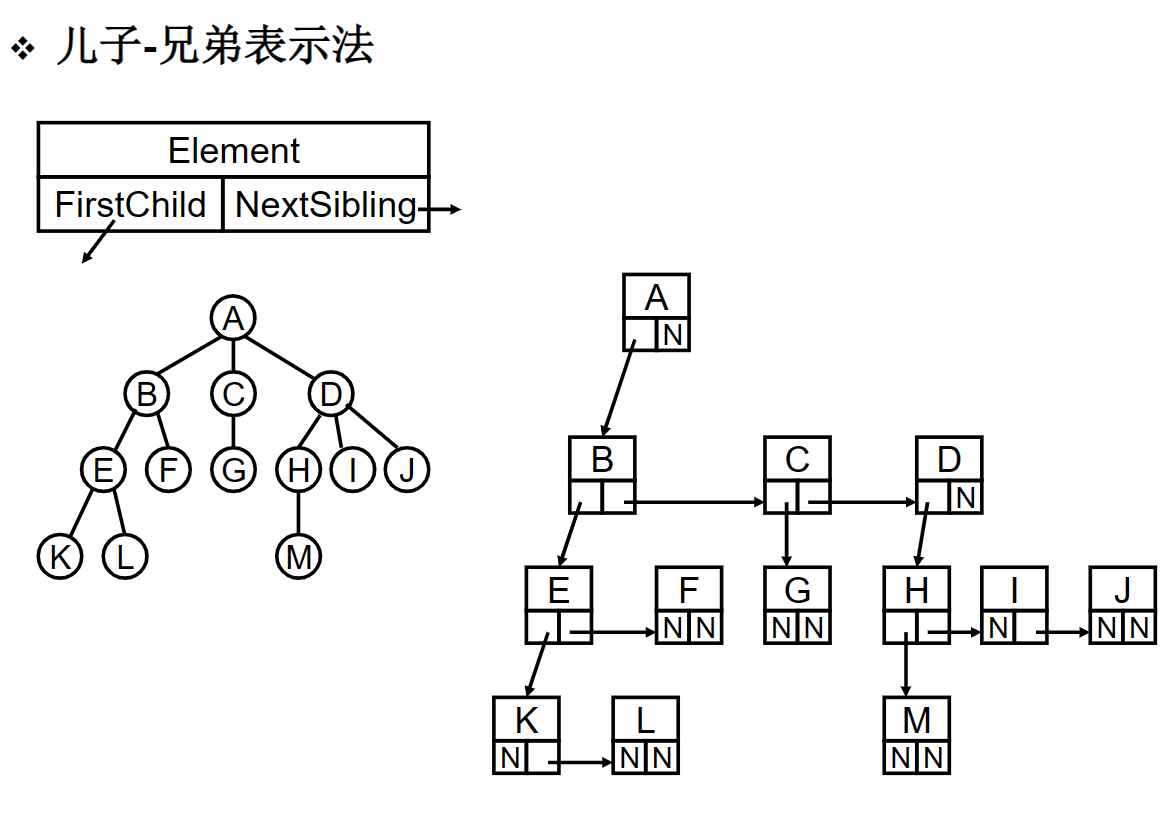
二叉树及存储结构

二叉树的定义和性质
定义：有穷的集合
- 集合可以为空
- 若不为空，则有左子树和右子树两个互不交叉的二叉树
性质：
- 一个二叉树第i层最大的结点数为2^i-1^ ,i>=1
- 深为k的二叉树最大的结点数为2^k-1^ ，k>=1
- 对于任意非空二叉树，n0代表叶结点个数，n2代表度数为2的非叶结点个数，那么满足n0=n2+1
二叉树的存储结构

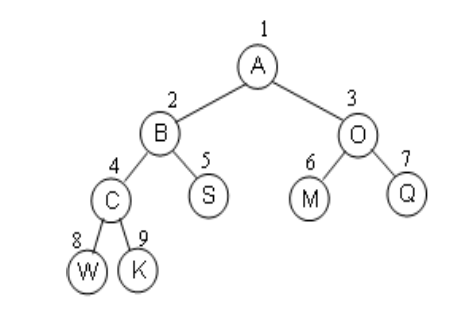
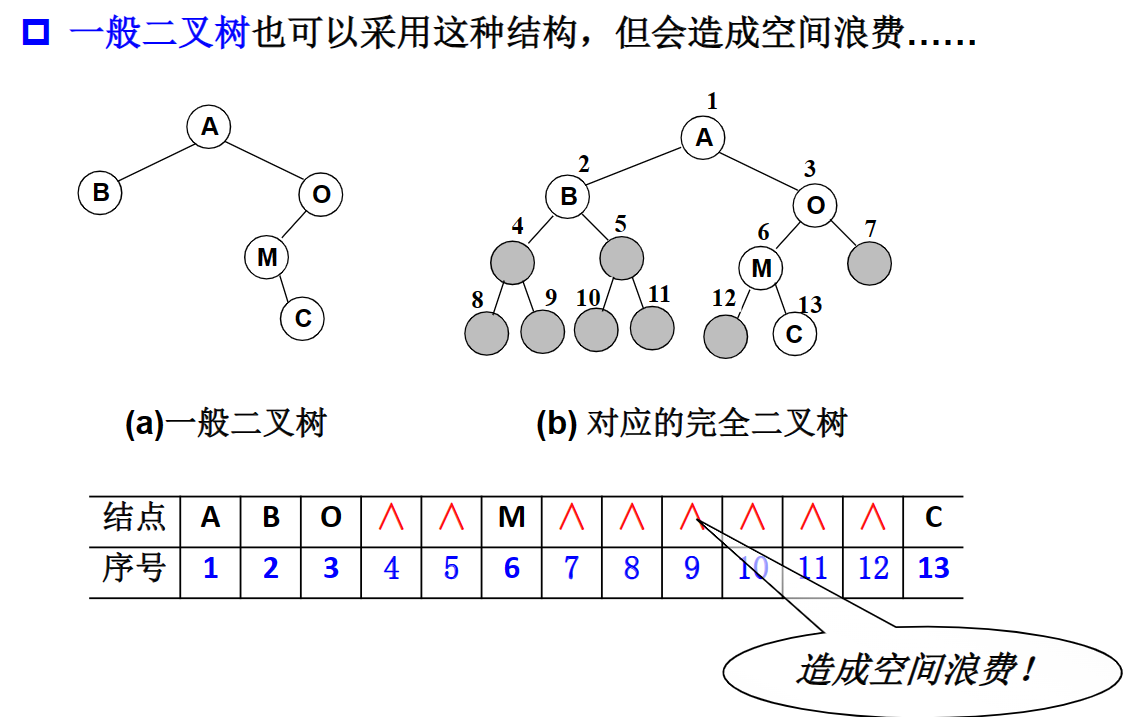
顺序存储结构
完全二叉树：按照从上到下，从左到右的顺序存储n个节点完全二叉树的父子结点关系
- 非根结点序号为i/2
- 序号结点为i的左孩子结点的序号为2i
- 序号结点为i的右孩子结点的序号为2i+1
- 一般二叉树采用此种存储方法会造成空间的浪费

链表存储结构

// 定义二叉树结点的结构体，使用 typedef 别名 BinTree 表示指向该结构体的指针类型
typedef struct TreeNode *BinTree;
// 使用别名 Position 表示指向二叉树结点的指针类型
typedef BinTree Position;
// 定义二叉树结点的结构体
struct TreeNode
{
    ElementType Data;   // 存储结点的数据
    BinTree Left;       // 左子树的指针
    BinTree Right;      // 右子树的指针
};

二叉树的遍历

先序中序后序

先序
访问根结点
遍历左子树
遍历右子树

// 前序遍历二叉树
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - 无，函数用于打印二叉树的前序遍历结果。
void PreorderTraversal(BinTree BT)
{
    // 判断当前结点是否为空
    if (BT)
    {
        // 如果当前结点不为空，打印当前结点的数据
        printf("%d ", BT->Data);
        // 递归遍历左子树
        PreorderTraversal(BT->Left);
        // 递归遍历右子树
        PreorderTraversal(BT->Right);
    }
}

中序
遍历左子树
访问根结点
遍历右子树

// 中序遍历二叉树
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - 无，函数用于打印二叉树的中序遍历结果。
void InorderTraversal(BinTree BT)
{
    // 判断当前结点是否为空
    if (BT)
    {
        // 递归遍历左子树
        InorderTraversal(BT->Left);
        // 如果当前结点不为空，打印当前结点的数据
        printf("%d ", BT->Data);
        // 递归遍历右子树
        InorderTraversal(BT->Right);
    }
}

后序
遍历左子树
遍历右子树
访问根结点

// 后序遍历二叉树
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - 无，函数用于打印二叉树的后序遍历结果。
void PostorderTraversal(BinTree BT)
{
    // 判断当前结点是否为空
    if (BT)
    {
        // 递归遍历左子树
        PostorderTraversal(BT->Left);
        // 递归遍历右子树
        PostorderTraversal(BT->Right);
        // 如果当前结点不为空，打印当前结点的数据
        printf("%d ", BT->Data);
    }
}

中序非递归
思路：利用堆栈

遇到一个结点就把它堆栈，然后遍历其左子树
遍历完左子树后将该结点弹出并访问
利用有指针中序遍历该结点右子树

// 中序遍历二叉树（非递归版本）
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - 无，函数用于打印二叉树的中序遍历结果。
void InorderTraversal(BinTree BT)
{
    BinTree T = BT;             // 定义辅助指针T，初始指向根结点
    Stack S = CreatStack(MaxSize); // 创建一个栈S，用于辅助遍历
    while (T || !isEmpty(S))    // 当T不为空或栈S不为空时继续遍历
    {
        while (T)              // 将指针T沿左子树一直向下，直到叶子结点
        {
            Push(S, T);        // 将结点指针T入栈
            T = T->Left;       // 移动指针T指向左孩子结点
        }
        if (!isEmpty(S))       // 当栈S不为空时，弹出栈顶元素
        {
            T = Pop(S);        // 弹出并取出栈顶元素，赋值给指针T
            printf("%5d", T->Data);  // 打印当前结点的数据
            T = T->Right;      // 将指针T指向当前结点的右孩子结点
        }
    }

层序

思路：利用队列
层序基本过程：遍历从根结点开始，首先将根结点入队，然后执行循环：结点出队，访问该结点，其左右儿子入队

// 层序遍历二叉树
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - 无，函数用于打印二叉树的层序遍历结果。
void LevelOrderTraversal(BinTree BT)
{
    BinTree T;          // 定义辅助指针T，用于遍历二叉树的结点
    Queue Q;            // 定义队列Q，用于存储待遍历的结点
    if (!BT) return;    // 若二叉树为空树，直接返回
    // 初始化队列
    Q = CreatQueue(MaxSize);
    AddQ(Q, BT);        // 将根结点入队列
    while (!isEmpty(Q))
    {
        // 取出队列的头结点，并访问该结点
        T = DeletQ(Q);
        printf("%5d", T->Data);
        // 如果当前结点有左子节点，将左子节点入队列
        if (T->Left) AddQ(Q, T->Left);
        // 如果当前结点有右子节点，将右子节点入队列
        if (T->Right) AddQ(Q, T->Right);
    }
}

例

求二叉树高度

// 中序遍历二叉树并计算二叉树的高度
// 参数：
//   - BinTree BT: 二叉树的根结点指针
// 返回值：
//   - int: 二叉树的高度
int InOrderTraversal(BinTree BT)
{
    int Hr, Hl, Maxh;
    if (BT)
    {
        // 递归遍历左子树，并获取左子树的高度
        Hl = InOrderTraversal(BT->Left);
        // 递归遍历右子树，并获取右子树的高度
        Hr = InOrderTraversal(BT->Right);
        // 计算当前树的高度，即左右子树高度的最大值加1（加1是因为要算上当前结点）
        Maxh = (Hl > Hr ? Hl : Hr) + 1;
        return Maxh;
    }
    else
    {
        // 代表该树为空树，高度为0
        return 0;
    }
}

第四章（树.中）

二叉搜索树

二叉搜索树又称为二叉排序树或二叉选择树

满足以下性质：

二叉树可以为空
非空左子树所有键值小于根结点键值
非空右子树所有键值大于根结点键值
左子树和右子树都是二叉搜索树

查找

从查找跟结点开始，若根结点为空，直接返回NULL
若根结点不为空，根结点关键字和X进行比较
- 若根节点键值大于X则从左子树继续搜索
- 若根节点键值小于X则从右子树继续搜索
- 若两者相等，搜索查找完成，结束

// 在二叉搜索树中查找元素 X
// 参数：
//   - ElementType X: 待查找的元素
//   - BinTree BT: 二叉搜索树的根结点指针
// 返回值：
//   - Position: 若找到元素 X，返回对应结点的指针，否则返回 NULL。
Position Find(ElementType X, BinTree BT)
{
    if (!BT) return NULL;   // 若当前结点为空树（NULL），说明未找到 X，返回 NULL
    if (BT->Data > X)
        return Find(X, BT->Left);   // 若当前结点值大于 X，说明 X 在左子树中，继续在左子树中查找
    else if (BT->Data < X)
        return Find(X, BT->Right);  // 若当前结点值小于 X，说明 X 在右子树中，继续在右子树中查找
    else
        return BT;   // 若当前结点值等于 X，说明找到了 X，返回当前结点指针
}

但非递归函数执行效率更高，可将递归函数改为迭代函数

// 在二叉搜索树中循环查找元素 X
// 参数：
//   - ElementType X: 待查找的元素
//   - BinTree BT: 二叉搜索树的根结点指针
// 返回值：
//   - Position: 若找到元素 X，返回对应结点的指针，否则返回 NULL。
Position InterFind(ElementType X, BinTree BT)
{
    while (BT)
    {
        if (BT->Data > X)
            BT = BT->Left;   // 如果当前结点值大于 X，说明 X 在当前结点的左子树中，移动到左子树继续查找
        else if (BT->Data < X)
            BT = BT->Right;  // 如果当前结点值小于 X，说明 X 在当前结点的右子树中，移动到右子树继续查找
        else
            return BT;   // 如果当前结点值等于 X，说明找到了 X，返回当前结点指针
    }
    // 如果树为空，返回 NULL
    return NULL;
}

最大元素一定在最右分支端结点上

最小元素一定在最左分支端结点上

查找最小元素递归

// 递归查找二叉搜索树中的最小元素
// 参数：
//   - BinTree BT: 二叉搜索树的根结点指针
// 返回值：
//   - Position: 返回最小元素所在结点的指针，若树为空则返回 NULL。
Position FindMin(BinTree BT)
{
    if (!BT) return NULL;  // 若当前结点为空树（NULL），说明树为空，直接返回 NULL
    // 若当前结点的左子树为空，说明当前结点为最小元素所在结点，直接返回当前结点指针
    else if (!BT->Left) return BT;
    // 否则递归调用 FindMin 函数，在当前结点的左子树中继续查找最小元素
    else return FindMin(BT->Left);
}

查找最大元素迭代

// 迭代查找二叉搜索树中的最大元素
// 参数：
//   - BinTree BT: 二叉搜索树的根结点指针
// 返回值：
//   - Position: 返回最大元素所在结点的指针，若树为空则返回 NULL。
Position FindMax(BinTree BT)
{
    if (BT)
    {
        // 沿右结点查找，直到最右叶结点
        while (BT->Right)
            BT = BT->Right;
    }
    return BT;
}

插入
方法类似find

// 向二叉搜索树中插入元素 X
// 参数：
//   - ElementType X: 要插入的元素值
//   - BinTree BST: 二叉搜索树的根结点指针
// 返回值：
//   - BinTree: 返回插入后的二叉搜索树的根结点指针
BinTree Insert(ElementType X, BinTree BST)
{
    // 若该树为空，生成并返回一个只包含一个结点的二叉树
    if (!BST)
    {
        BST = malloc(sizeof(struct TreeNode));
        BST->Data = X;
        BST->Right = BST->Left = NULL; //将新结点的左右子树指针初始化为空。
    }
    else
    {
        if (BST->Data > X)
            BST->Left = Insert(X, BST->Left); // 将 X 插入左子树
        else if (BST->Data < X)
            BST->Right = Insert(X, BST->Right); // 将 X 插入右子树
    }
    return BST;
}

3.删除
分三种情况

若删除的为叶结点，则直接删除，并将父结点指针置为NULL
若删除的结点只有一个孩子结点，则将父结点指向要删除结点的孩子结点

若要删除的结点有左右两颗子树，则用其他结点替代要删除的结点，左子树的最大元素或者右子树的最小元素

// 从二叉搜索树中删除元素 X
// 参数：
//   - ElementType X: 要删除的元素值
//   - BinTree BST: 二叉搜索树的根结点指针
// 返回值：
//   - BinTree: 返回删除元素后的二叉搜索树的根结点指针
BinTree Delete(ElementType X, BinTree BST)
{
    Position Tmp;
    // 若树为空，表示未找到要删除的元素 X，打印提示信息并直接返回
    if (!BST)
    {
        printf("未查找到");
        return NULL;
    }
    else if (BST->Data > X)
        BST->Left = Delete(X, BST->Left); // 在左子树中继续查找并删除元素 X
    else if (BST->Data < X)
        BST->Right = Delete(X, BST->Right); // 在右子树中继续查找并删除元素 X
    else
    {
        // 找到要删除的结点

        // 被删除的结点有左右两个子结点
        if (BST->Left && BST->Right)
        {
            Tmp = FindMin(BST->Right);
            // 用右子树中最小值替代被删除结点的值
            BST->Data = Tmp->Data;
            BST->Right = Delete(BST->Data, BST->Right);
        }
        else
        {
            // 被删除的结点有一个或无子结点

            Tmp = BST;
            // 如果左边是空的，则把右边指针指向父亲结点
            if (!BST->Left)
                BST = BST->Right;
            else if (!BST->Right)
                BST = BST->Left;
            free(Tmp);
        }
    }
    return BST;
}

平衡二叉树

平衡因子BF(T)= h_L- h_R,其中h_L和h_R分别为左右子树高度
平衡二叉树：空树，或者任一结点左右子树高度差的绝对值不超过1
即|BF(T)|<=1

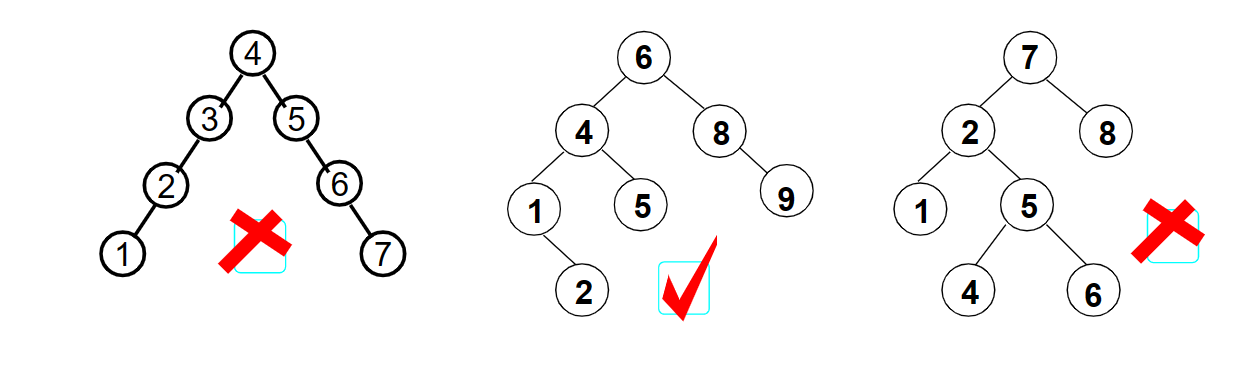
给定结点树为n的avl树的最大高度为O(log2n)

平衡二叉树的调整：

判断被破坏点的位置确定旋转方向

RR旋转

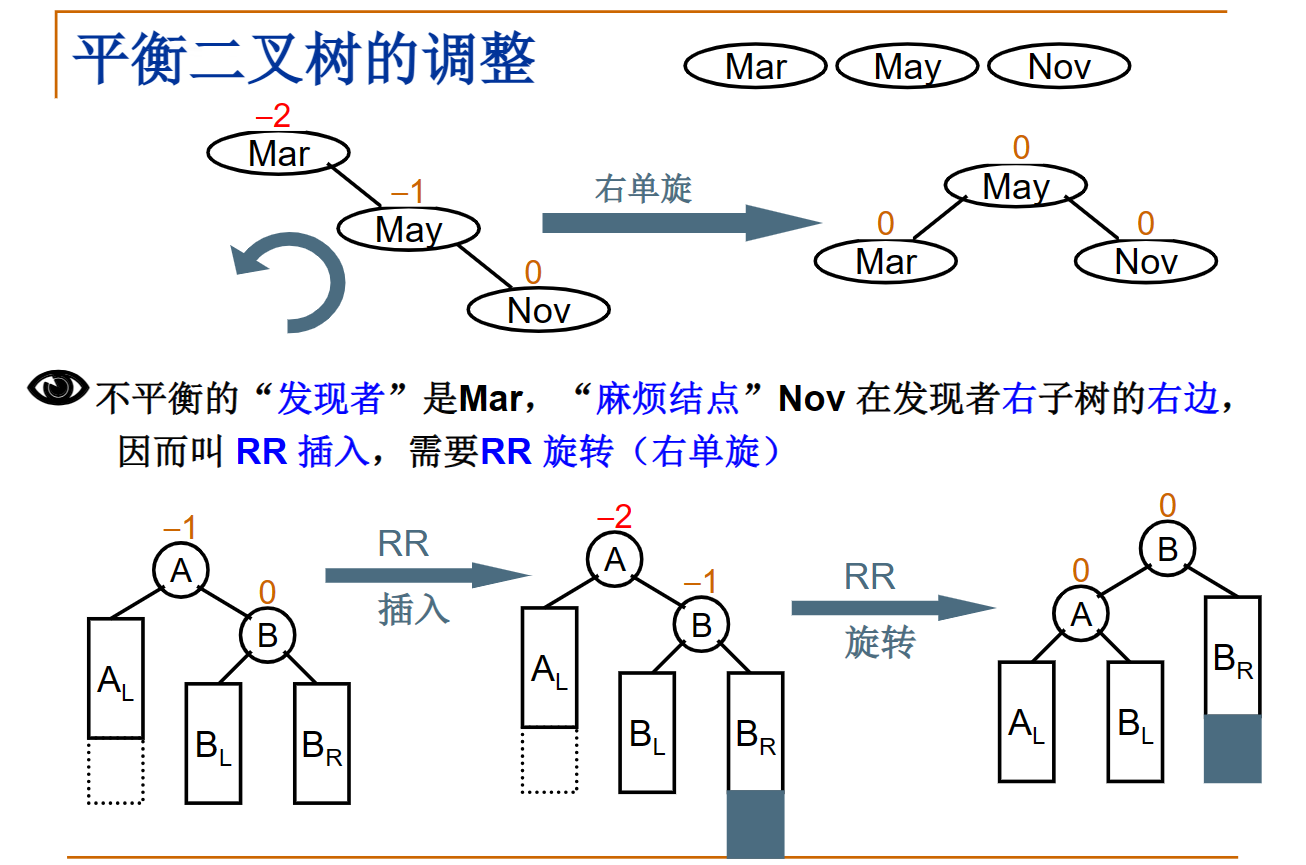
LL旋转

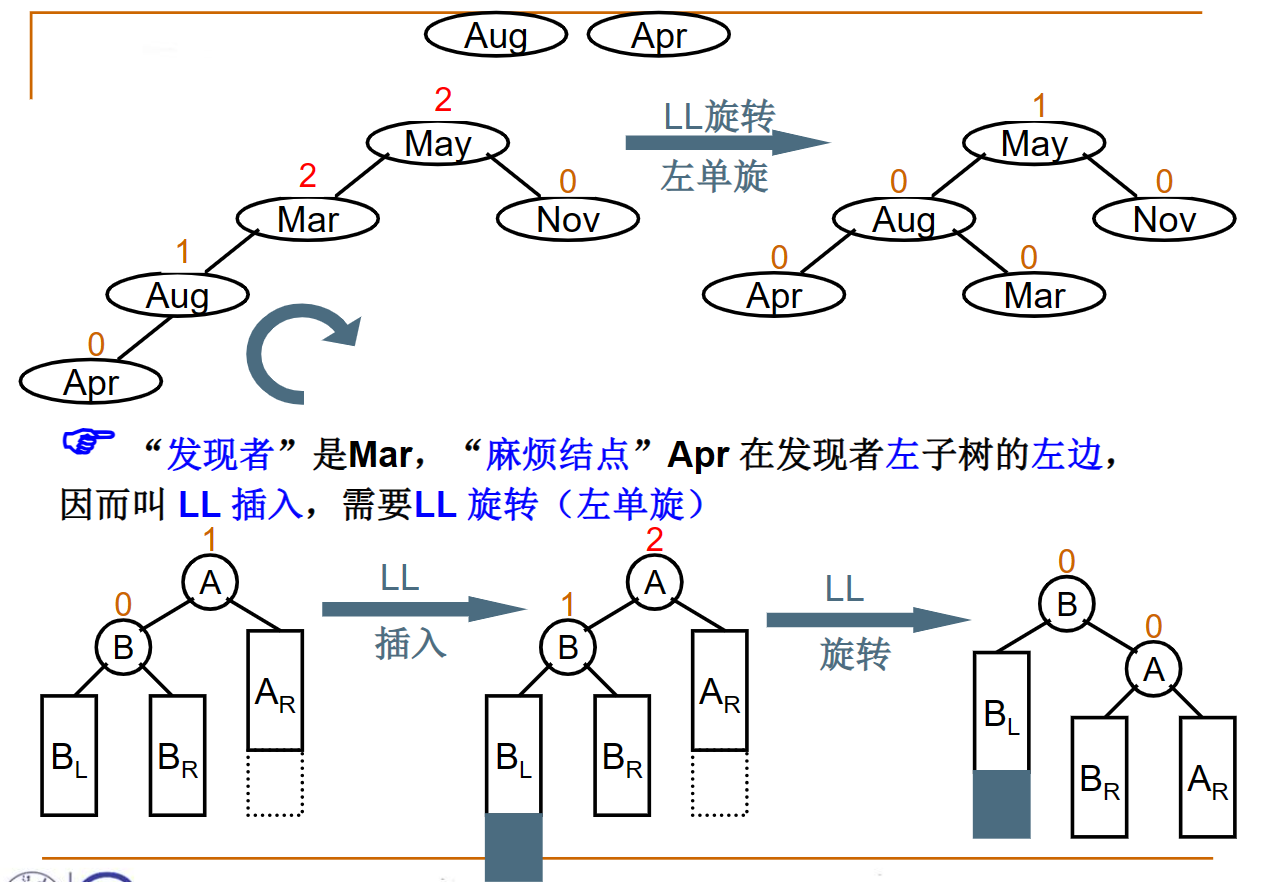
LR旋转

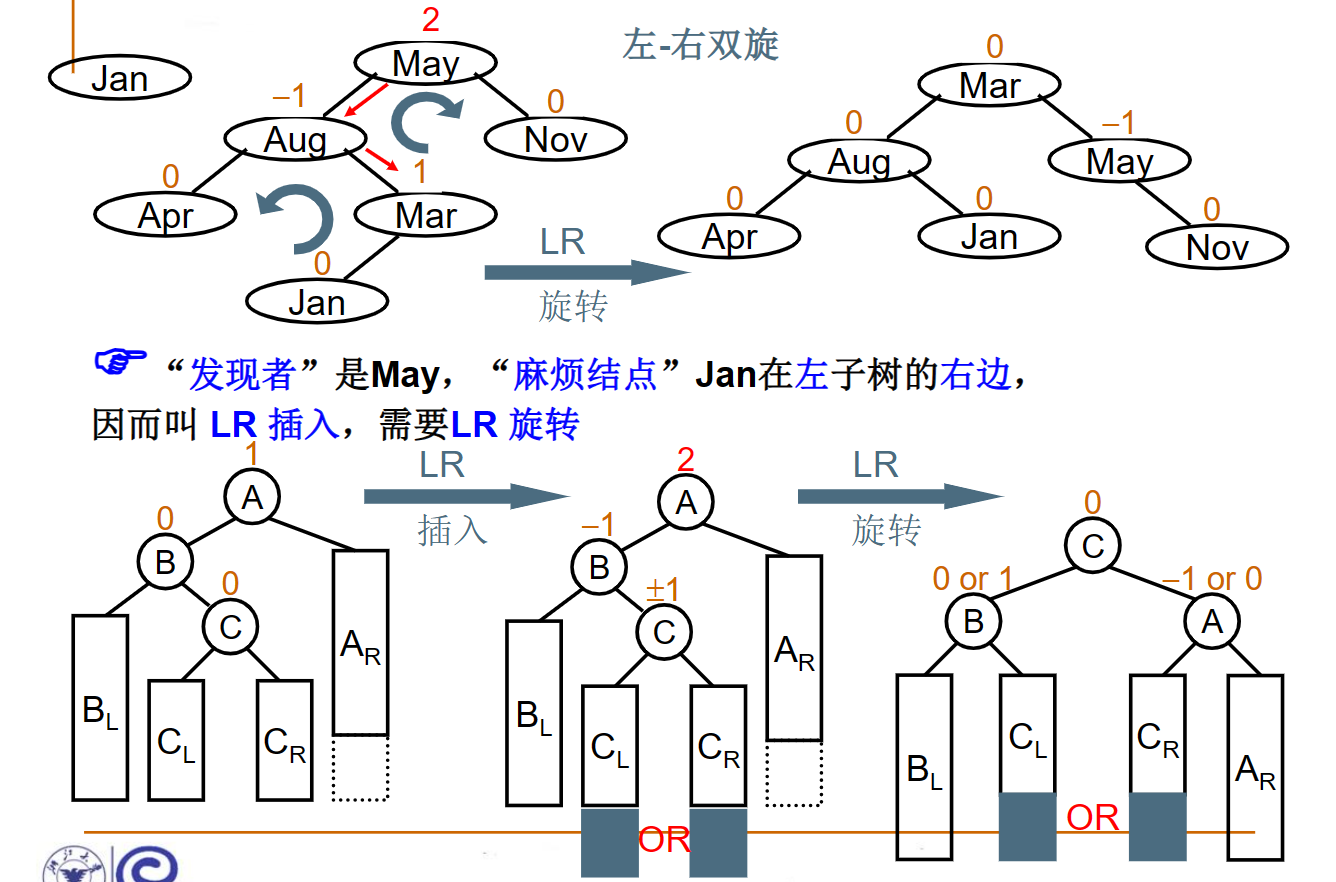
RL旋转

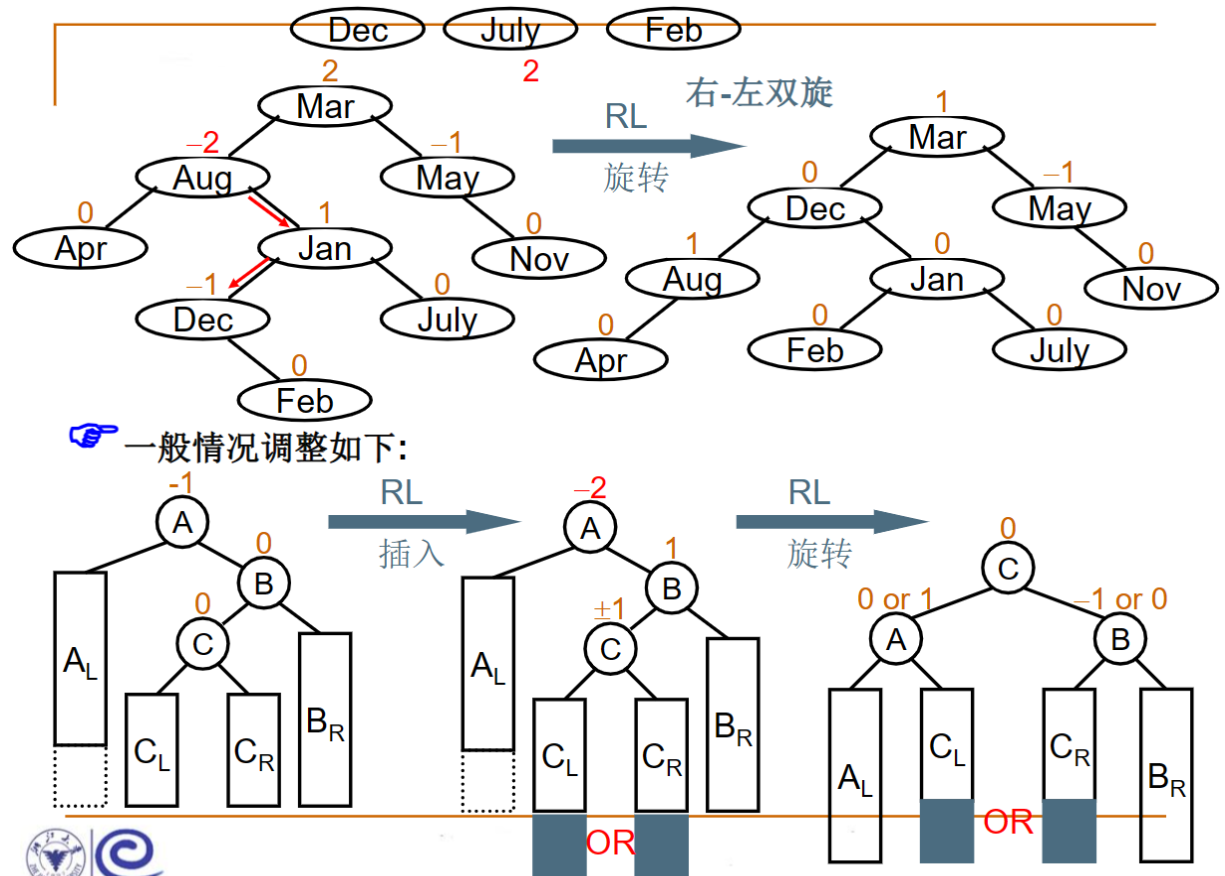
小白专场（空）

第五章（树.下）

堆

优先队列：特殊的队列，取出元素的顺序时依照元素的优先权大小，而不是元素进入队列的先后顺序优先队列的完全二叉树
结构性：用数组表示的完全二叉树
有序性：任一结点的关键字是其子树所有结点的最大值或者最小值
抽象数据描述：

最大堆创建

typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
    // 存储堆元素的数组
    ElementType *Elements;
    // 堆当前元素个数
    int Size;
    // 堆的最大容量
    int Capacity;
}
// 创建最大堆
MaxHeap CreateMaxHeap(int MaxSize)
{
    // 分配内存空间用于存储最大堆
    MaxHeap H = malloc(sizeof(struct HeapStruct));
    // 分配内存空间用于存储堆元素的数组
    H->Elements = malloc((MaxSize + 1) * sizeof(ElementType));
    // 初始化堆的相关属性
    H->Size = 0;
    H->Capacity = MaxSize;
    // 设置哨兵，哨兵的值为最大可能的元素值
    H->Elements[0] = MaxData;
    return H;
}

最大堆的插入
将新增结点插入到从父结点到跟结点的有序序列中

// 向最大堆中插入元素
void insert(MaxHeap H, ElementType item)
{
    int i;
    // 判断最大堆是否已满
    if (isFull(H))
    {
        printf("最大堆已满");
        return;
    }
    // 将元素插入堆的末尾
    i = ++H->Size;
    // 向上调整结点，找到插入位置
    for (; H->Elements[i / 2] < item; i /= 2)
    {
        // 将父结点的值下滤到当前结点
        H->Elements[i] = H->Elements[i / 2];
    } 
    // 将元素插入到找到的位置
    H->Elements[i] = item;
}

最大堆的删除
取出根结点最大值元素，同时删除堆的一个结点

// 从最大堆中删除最大元素
ElementType DeletMax(MaxHeap H)
{
    int Parent, Child;
    ElementType MaxItem, temp;
    // 判断最大堆是否为空
    if (IsEmpty(H))
    {
        printf("最大堆已空");
        return;
    }   
    // 取出根结点最大值，用最大堆中最后一个元素从根结点开始向下过滤下层结点
    MaxItem = H->Elements[1];
    temp = H->Elements[H->Size--];
    for (Parent = 1; Parent * 2 <= H->Size; Parent = Child)
    {
        // 将Child指向左右儿子中较大的一个
        Child = Parent * 2;
        // 如果有右儿子并且右儿子的值大于左儿子，则Child指向右儿子
        if ((Child != H->Size) && (H->Elements[Child] < H->Elements[Child + 1]))
            Child++;
        // 如果temp的值大于等于Child结点的值，则找到了temp应该插入的位置，退出循环
        if (temp >= H->Elements[Child])
            break;
        else
            // 将较大的Child结点上滤到Parent结点位置
            H->Elements[Parent] = H->Elements[Child];
    }
    // 将temp插入到找到的位置
    H->Elements[Parent] = temp;
    return MaxItem;
}

最大堆的建立：
将已经存在的N个元素按照最大堆的要求存放在一个一维数组中

线性复杂度下建立最大堆

N个元素按线性存入，完全满足二叉树结构特性

调整各个结点的位置，以满足最大堆的有序性

哈弗曼树

例：将百分制成绩转换为五分制成绩
结点不同的查找频率可构造更加有效的生成树

哈夫曼树的定义
带权路径长度（WPL）：设二叉树有n个叶子结点，每个叶子结点带有权值wk，从根节点到每个叶子结点的长度为lk，则每个叶子结点的带权路径长度之和为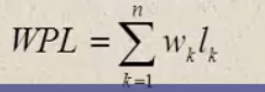

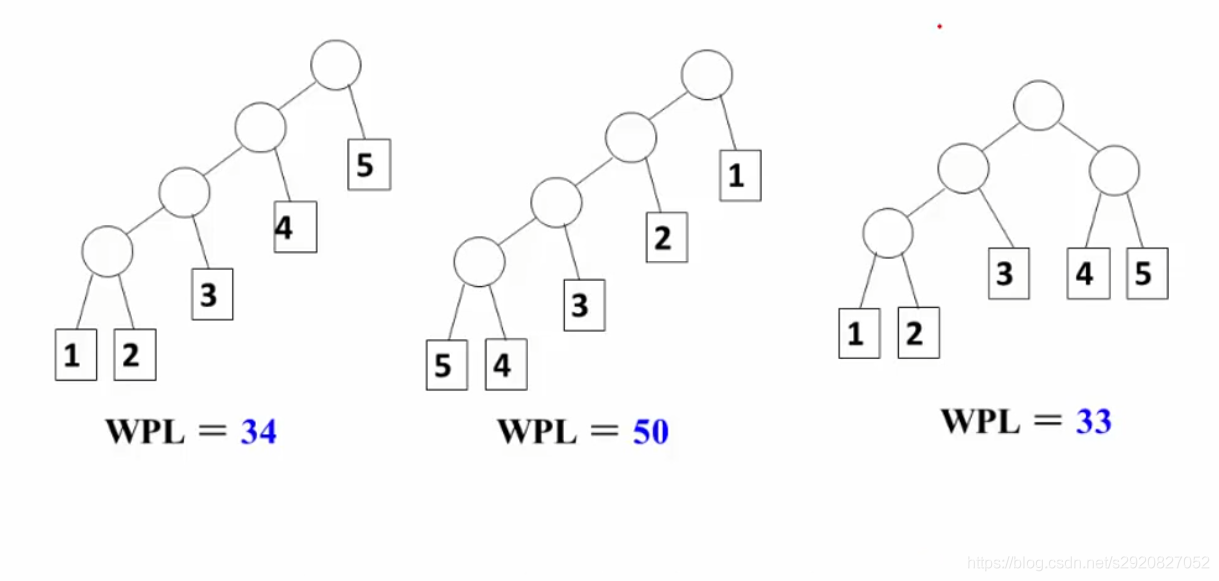
哈弗曼树在做一个问题，如何排序结点使得WPL值最小

哈夫曼树的构造

每次把权值最小的两棵树合并

typedef struct TreeNode *HuffmanTree;
struct TreeNode {
    int Weight; // 结点的权值
    HuffmanTree Left, Right; // 左右子树的指针
};
// 哈夫曼树的构建
HuffmanTree Huffman(MinHeap H) {
    // 假设H->Size个权值已经存在H->Elements[]->Weight中
    int i;
    HuffmanTree T;
    BuildMinHeap(H); // 将最小堆转换为最小优先队列
    // 通过贪心算法构建哈夫曼树
    for (i = 1; i < H->Size; i++) {
        // 建立新结点
        T = malloc(sizeof(struct TreeNode));
        T->Left = DeleteMin(H); // 从最小优先队列中删除最小权值的结点作为左子树
        T->Right = DeleteMin(H); // 从最小优先队列中删除次小权值的结点作为右子树
        T->Weight = T->Left->Weight + T->Right->Weight; // 计算新结点的权值
        Insert(H, T); // 将新结点插入最小优先队列
    }

    T = DeleteMin(H); // 最小优先队列中最后剩下的结点即为哈夫曼树的根结点
    return T;
}
// 时间复杂度: NlogN

哈夫曼树的特点：

没有度为一的结点
n个叶子结点的哈夫曼树共有2n-1个结点
哈夫曼树任意非叶节点的左右子树交换后仍是哈夫曼树

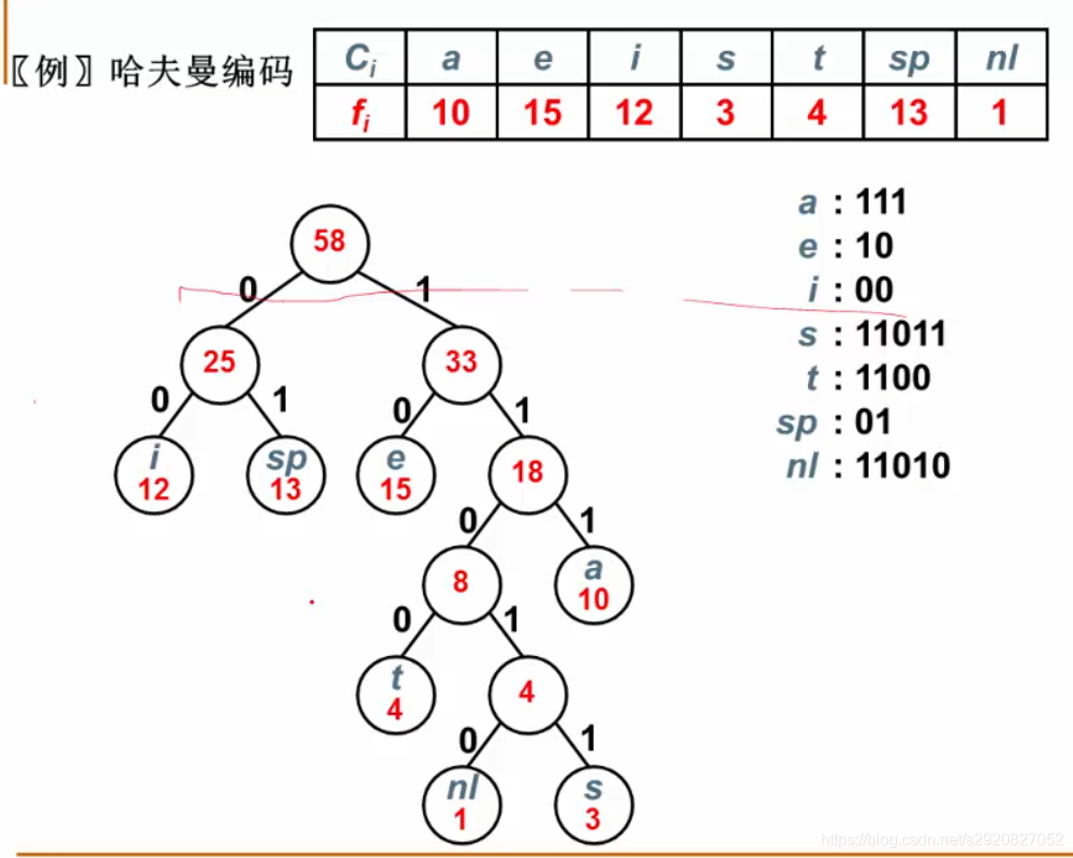
哈夫曼树和哈夫曼编码

不等长编码：出现频率高的字符用的编码短些，出现频率低的字符用的编码高些

如何进行不等长编码？

编码可能出现二义性，根据二义性引出前缀码的概念：任何字符的编码都不是另一字符编码的前缀

可以无义地解码

二叉树用于编码：
左右分支0，1
字符只在叶结点上

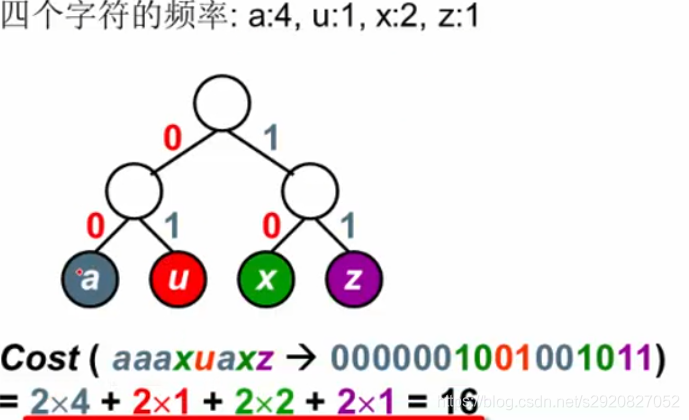
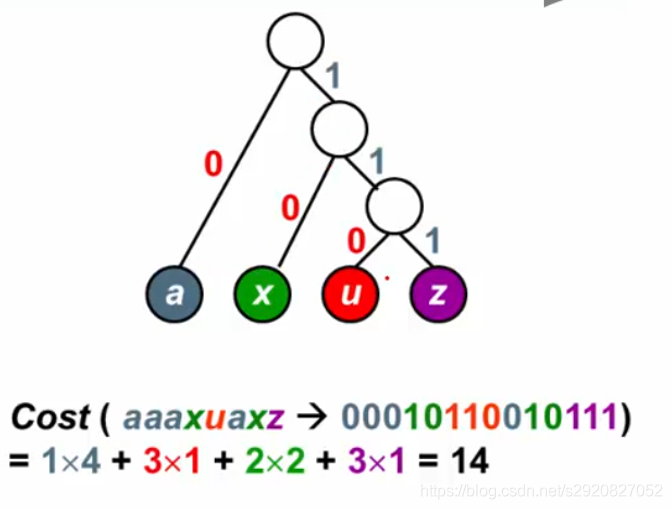
用哈夫曼树可以实现二叉树编码代价最小

集合及运算

集合可以用数组存储

查找某个元素的集合

int Find(SetType S[],ElementType X)
{
	//在数组中查找值为X的元素所属集合
	//MaxSize是全局变量，为数组S的最大长度
	int i;
	for(int i = 0; i < MaxSize && S[i].Data != X; i ++)
	if(i>=MaxSize)return -1;
	for(;S[i]->Parent>=0;i = S[i].Parent);
	return i;
}

集合的并运算

分别找到X1和X2两个元素所在集合的根结点
如果他们不同根，则将一个根结点的父结点指针设置为另一个根结点的数组下标
1
2
3
4
5
6
7
8
void Union(SetType S[],ElementType X1,ElementType X2)
{
int Root1,Root2;
Root1 = Find(S,X1);
Root2 = Find(S,X2);
if(Root1!=Root2)
S[Root2].Parent=Root1;
}
为了改善合并以后的查找性能，可以采取小的集合合并到大的集合中，可以修改union函数，即将第一个结点的Parent修改为负的元素个数，对应其绝对值即为元素个数，方便比较

第六章(图.上)

图

图的定义:

六度空间理论(Six Degrees of Separation)
任何两个人之间不超六个人之间认识

图可以解决的问题

花费最少可以转换为最小生成树的问题

线性表和树可以描述为图的一个特殊情况

表示多对多的关系
包含:

一组顶点：通常用V(Vertex)表示顶点集合

一组边：通常用E(Edge)表示边的集合
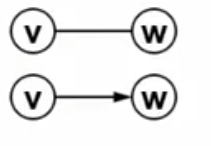
边是顶点对：(v,w)属于E,其中v,w属于V v——w
有向边<v,w>表示从v指向w的边（单行线）v——> w
不考虑重边和自回路

抽象数据类型定义：

常见术语：

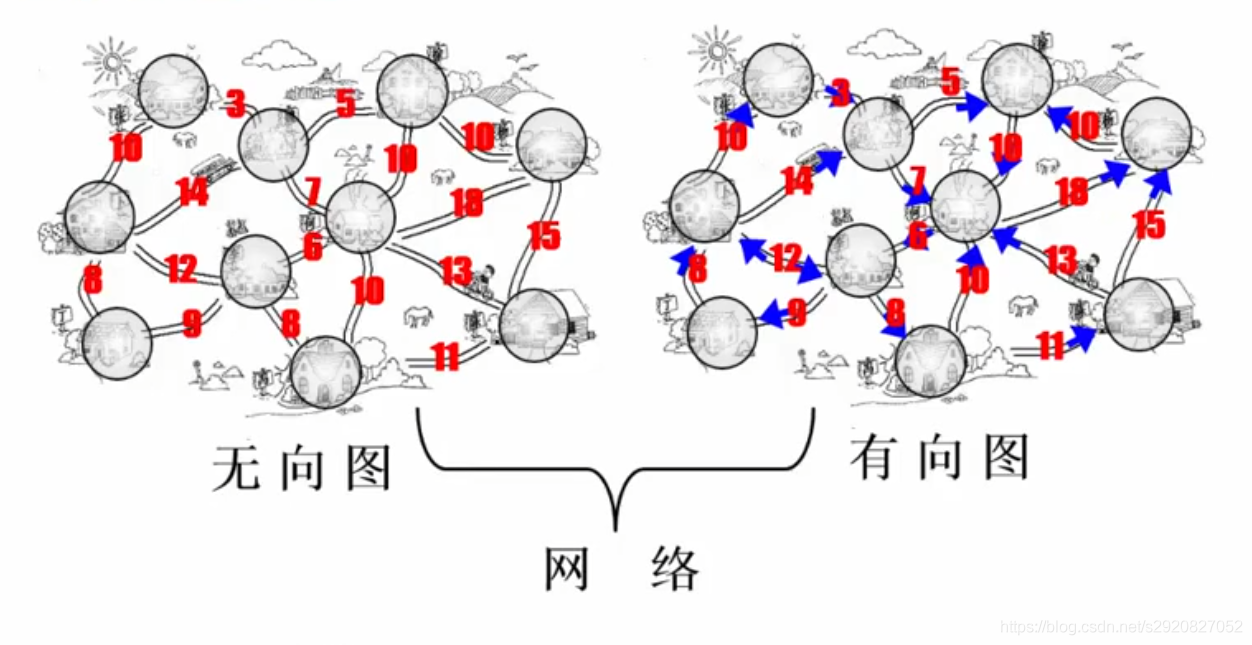
红色数字称为权重,有权重的我们称之为网络

邻接矩阵表示法

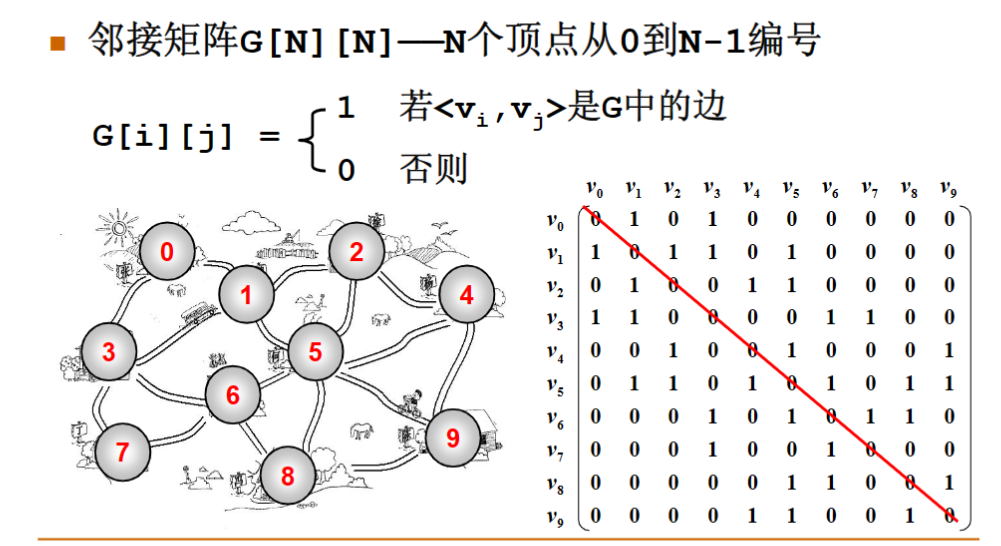
邻接矩阵是对称的，只需要存一半的元素即可，省去一半的存储空间

浪费空间：存稀疏图（点很多而边很少）有大量无效元素
对于稠密图，特别是稀疏图比较合算

邻接表表示法

邻接表：G[N]是指针数组，对应矩阵每一行一个链表，只存非零元素，顺序没有要求

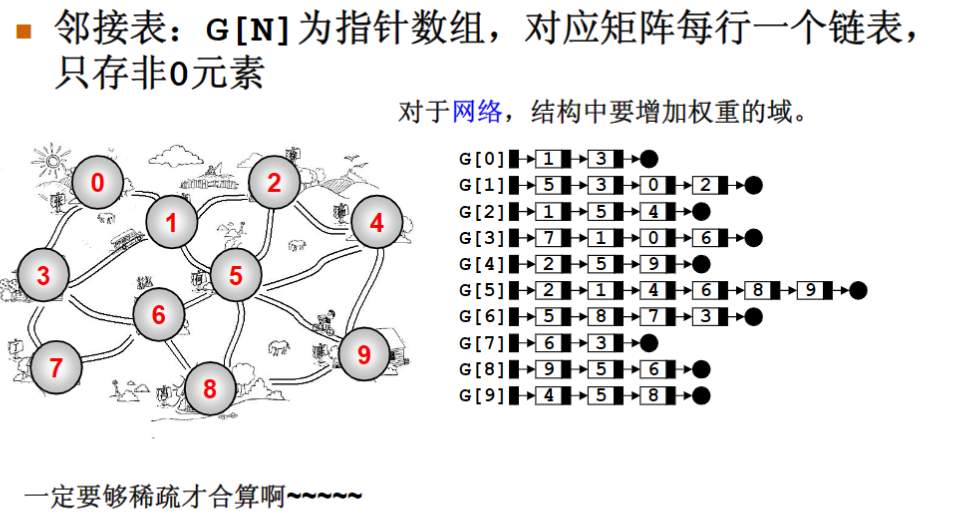
方便找任一顶点的所有”邻接点“

节约稀疏图空间
需要N个头指针和2E个结点（每个结点至少需要连个域）

图的遍历

DFS 深度优先搜索

N条边E个结点
邻接表存图O(N+E)
邻接矩阵存图O(N2)

BFS 广度优先搜索

为什么两种遍历?

图连不通怎么办?

连通：如果v到w存在一条（无向）路径，则称v到w是连通的
路径：v到w的路径是一系列顶点（v,v1,v2,v3,vn,w）,其中任意相邻顶点间都有图中的边。路径的长度是路径中的边数（如果带权，是所有边数权重之和）。如果v到w是所有顶点都不同，则称之为简单路径。
回路：起点等于终点的路径
连通图；图中任意两点均连通
连通分量：无向图的极大连通子图
极大顶点数：再加一个顶点就不连通的
极大边数：包含子图中所有顶点相连的所有边
强连通：有向图中顶点v和w之间存在双向路径，则称v和w强连通
强连通图：有向图中任意两顶点均强连
强连通分量：有向图的极大强连通子图
每调用一次DFS(V),就把V所在连通分量遍历一遍，BFS(V)也是一样

拯救007

void save007(Graph G)
{
for(each V in G)
{
if(!visited[G]&&FirstJump(G))
{
answer = DFS(V);
if(answer==YES)break;
}
}
if(answer==YES)output(“Yes”);
else output(“No”);
}

void DFS(Vertex V)
{
visited[V]=true;
if(IsSafe(V))answer = YES;
else
{
//for(V的每个邻接点W)
for(each W in G)
if(!visited[W]&&Jump(V,W))
{
answer = DFS(W);
if(answer==YES)break;
}
}
return answer;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
六度空间

算法思路：
对每个节点进行广度优先搜索
搜索过程累计访问的节点
需要记录“层数”，仅计算6层以内结点数

int BFS(Vertex V)
{
visited[V] = true; count = 1;
level = 0; last = V;
Enqueue(V,Q);
while(!IsEmpty(Q))
{
V = Dequeue(Q);
for(V每个邻接点W)
if(!visited[W])
{
visited[W] = true;
Enqueue(W,Q);
count++;
tail = W;
}
if(V==last)
{
level++;
last = tail;
}
if(level == 6)break;
}
return count;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

邻接矩阵表示的图

创建一个图

typedef struct GNode *PtrToGNode;
struct GNode{
	int Nv;//顶点数
	int Ne;//边数
	WeightType G[MaxVertexNum][MaxVertexNum];
	DataType Data[MaxVertexNum];
};
typedef PtrToGNode MGraph;//以邻接矩阵存储图的类型

MGraph 初始化

初始化一个有VertexNum个顶点但是没有边的图

MGraph CreatGraph(int VertexNum)
{
	MGraph Graph;
	Graph = (MGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	for(V = 0; V < Graph->Nv; V ++)
	for(W = 0; W < Graph->Ne; W ++)
	Graph->G[V][W] = 0;
	//如果有权值可以使Graph->G[V][W]=INFINITY;
	return Graph;
}

向MGraph插入一条边

typedef struct  ENode *PtrToENode;
struct ENode{
	Vertex V1,V2;//有向边V1，V2
	WeightType Weight;//权重
};
typedef PtrToENode Edge;
//把相应的权重赋值给相应的邻接矩阵
void InsertEdge(MGraph Graph,Edge E)
{
	//有向图
	Graph->G[E->V1][E->V2] = E->Weight;
	//若为无向图还需要插入一条V2V1边
	Graph->G[E->V2][E->V1] = E->Weight;
}

完整建立一个MGraph

int G[MAXN][MAXN],Nv,Ne;
void BuildGraph()
{
	int i,j,v1,v2,w;
	scanf("%d",&Nv);
	for( i = 0; i < Nv; i ++)
	for( j = 0; j < Nv; j ++)
	G[i][j] = 0;
	scanf("%d",&Ne);
	for( i = 0; i < Ne; i ++)
	{
		scanf("%d %d %d",&v1,&v2,&w);
		G[v1][v2]=w;
		G[v2][v1]=w;
	}
}

用邻接表表示的图

邻接表：G[N]是指针数组，对应矩阵每行一个链表，只存非零元素

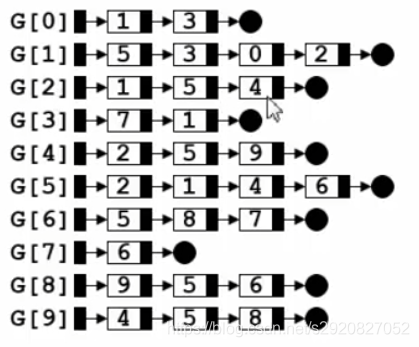
typedef struct GNode *PtrToGNode;
struct GNode{
	int Nv;
	int Ne;
	AdjList G;
	//邻接表
};
typedef PtrToGNode LGraph;

typedef struct Vnode{
	PtrToAdjVNode FirstEdge;
	DataType Data;
}AdjList[MaxVertexNum];
//AdjList 邻接表类型

typedef struct AdjVNode PtrToAdjVNode;
struct AdjVNode{
	Vertex AdjV;//邻接表下标
	WeightType Weight;
	PtrToAdjVNode Next;
}

初始化

LGraph CreatGraph(int VertexNum)
{
	Vertex V,W;
	LGraph Graph;
	Graph = (LGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	
	for( V = 0; V < Graph->Nv; V ++)
	Graph->G[V].FirstEdeg = NULL;
	return Graph;
}

插入边

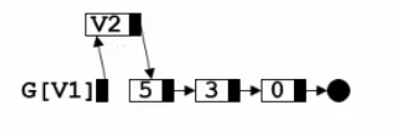
void InsertEdge(LGraph Graph,Edge E)
{
	PtrToAdjVNode NewNode;
	
	//给V2建立新结点
	NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
	NewNode->AdjV = E->V2;
	NewNode->Weight = E->Weight;
	//将V2插入V1表头
	NewNode->Next = Graph->G[E->V1].FirstEdge;
	Graph->G[E->V1].FirstEdge = NewNode;
	
	//若是无向图，则需要插入V2V1边
	//给V1建立新结点
	NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
	NewNode->AdjV = E->V1;
	NewNode->Weight = E->Weight;
	//将V1插入V2表头
	NewNode->Next = Graph->G[E->V2].FirstEdge;
	Graph->G[E->V2].FirstEdge = NewNode;
}

第七章（图.中）

第八章（图.下）

最小生成树问题

==什么是最小生成树？==

时一棵树
- 无回路
- |v|个顶点有v-1条边
是生成树
- 包含全部顶点
- v-1条边全部在图里
边的权重和最小

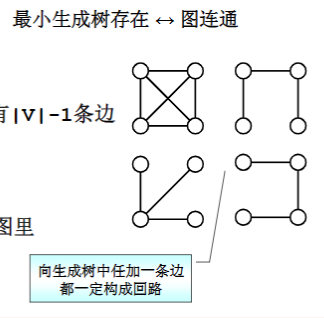
贪心算法（Prim和Kruskal）:

贪：每一步都要最好的
好：权重最小的边
- 需要约束：
  - 只用图中的边
  - 用完V-1条边
  - 不能有回路

Prim算法(稠密图)

核心思想：从一个初始节点开始，逐步扩展生成树，每次选择一条连接已选择节点和未选择节点的最短边，确保生成树的连通性，并保持总权重最小。不断重复这个过程，直到生成树包含了所有节点为止，最终得到最小生成树。

让小树长大

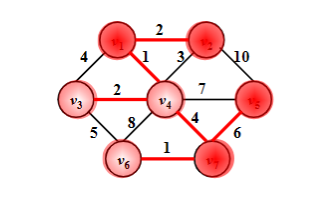
Kruskal算法(稀疏图)

核心思想：以边为中心，通过不断选择权重最小的边，并确保不形成环路来构建最小生成树，是一种有效且常用的解决最小生成树问题的方法。

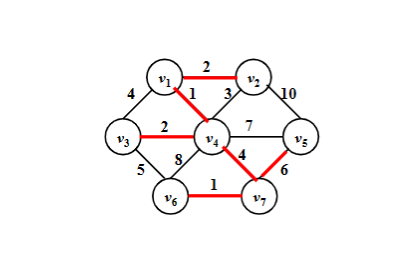
拓扑排序

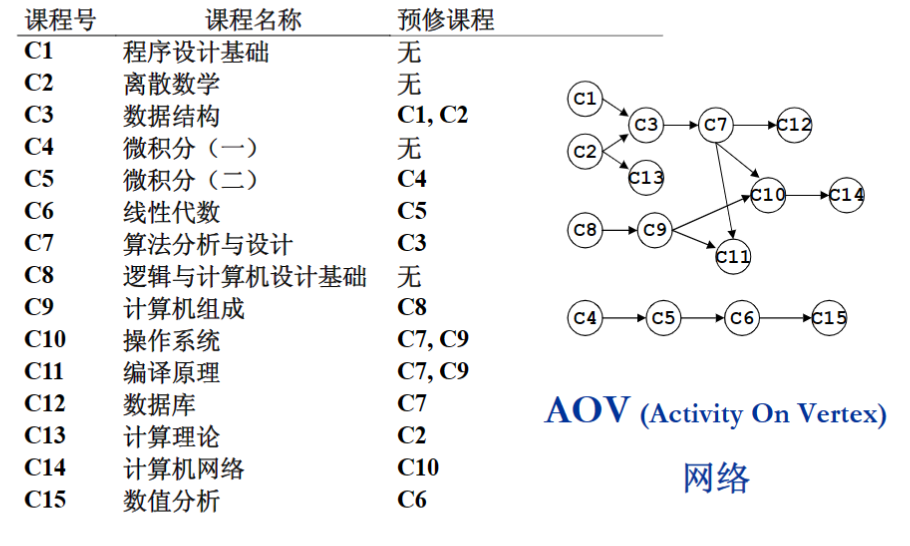
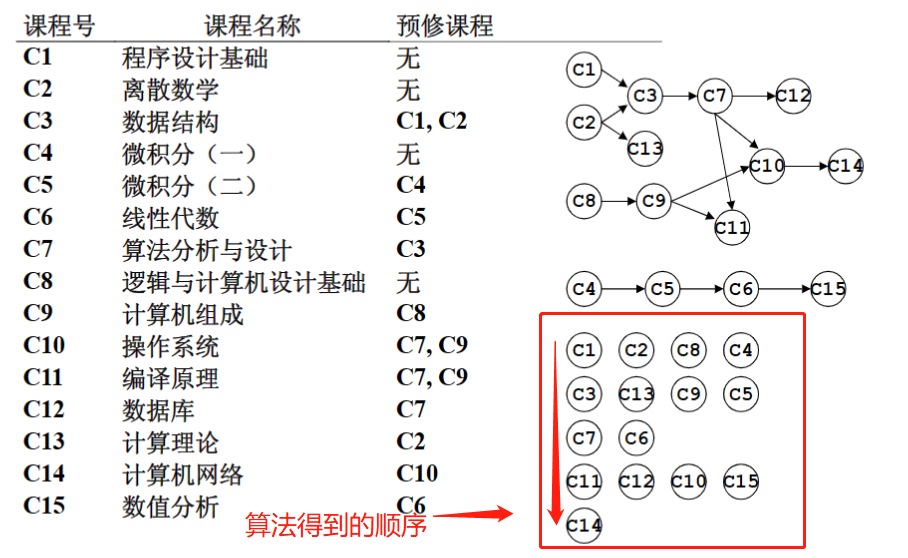
拓扑序：如果图中从v到w有一条有向路径，则v一定在w前，满足此条件的顶点序成为拓扑序
获取一个拓扑序的过程就是拓扑序列
AOV如果有合理的拓扑序，则必定是有向无环图

👆比较笨的算法

👇相对聪明的算法

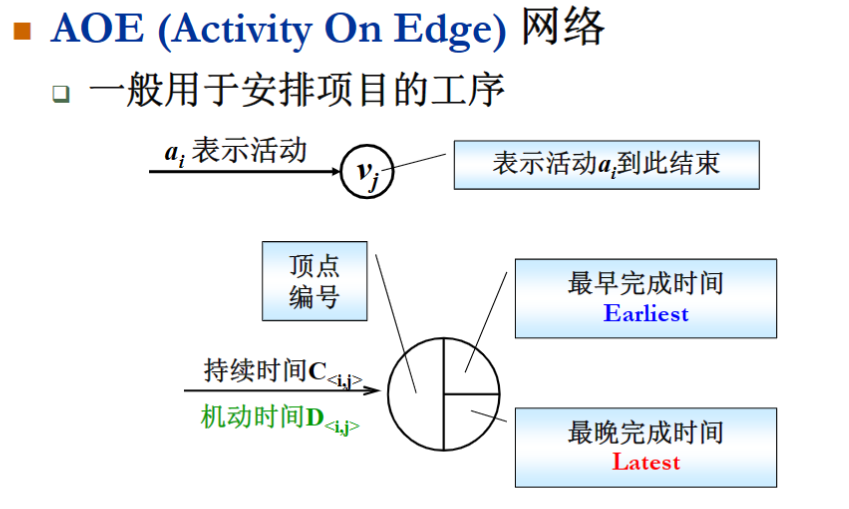
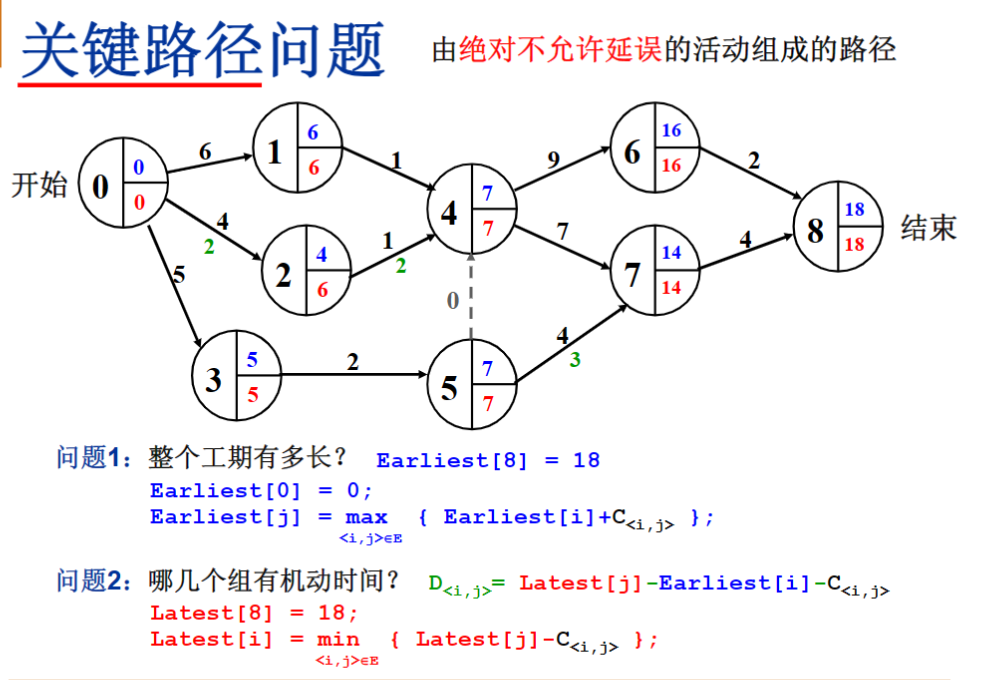
第九章（排序.上）

简单排序

==什么是简单排序？==

void X_Sort(ElementType A[],N)

大多数情况下，为了简单起见，讨论从小到大排序
N是正整数
只基于比较的排序（<=>有定义）
只讨论内部排序
稳定性：任意两个相等的数据，排序前后相对位置不变
没有一种排序在任何情况下都是最好的

冒泡法

核心思想：通过不断交换相邻元素，将较大的元素逐渐“冒泡”到数组的末尾，同时较小的元素逐渐沉到数组的开头。

插入排序

核心思想：将待排序的数组分成已排序和未排序两部分，然后逐个将未排序部分的元素插入到已排序部分的合适位置，直到所有元素都被排序为止。

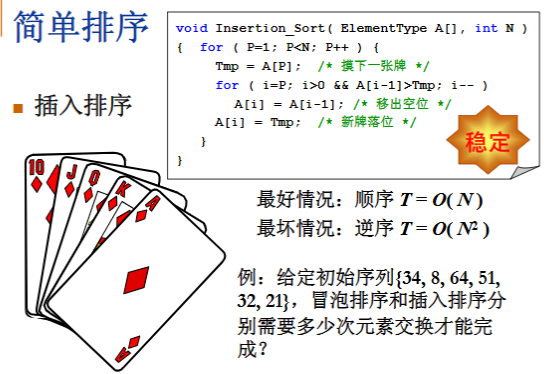
时间复杂度下界

对于下标 i<j ,如果A[i]>A[j],则称(i,j)为一对逆序对（inversion）
交换两个相邻元素正好消去一个逆序对
插入排序T(N,I)= O(N+I)
- 如果一个序列基本有序，那么插入排序比较高效
定理：任意N个不同元素组成的序列平均具有N(N-1)/4个逆序对
定理：任何仅以交换相邻两元素来排序的算法，其平均时间复杂度（N2）
这就意味着：如果想要提高算法效率，我们必须
- 每次消去不止一个逆序对
- 交换相隔较远的2个元素

希尔排序

希尔排序（Shell Sort）是一种高效的不稳定排序算法，它是插入排序的改进版本。

希尔排序的核心思想是通过将原始数组分割成多个子序列，然后对这些子序列进行插入排序，最终合并这些子序列，不断减小子序列的间隔，最终完成整个数组的排序。希尔排序的==关键==在于选择合适的间隔序列，这样可以在一定程度上提高排序的效率。

void Shell_Sort(ElementType A[], int N)
{
    int D, P, i;
    ElementType Tmp;
    // 希尔增量序列
    for (D = N / 2; D >= 1; D /= 2) {
        // 对每个子序列进行插入排序
        for (P = D; P < N; P++) {
            Tmp = A[P];
            // 在子序列中进行插入排序
            for (i = P; i >= D && A[i - D] > Tmp; i -= D) {
                A[i] = A[i - D];
            }
            A[i] = Tmp; // 插入元素到正确位置
        }
    }
}

==但是！！！==

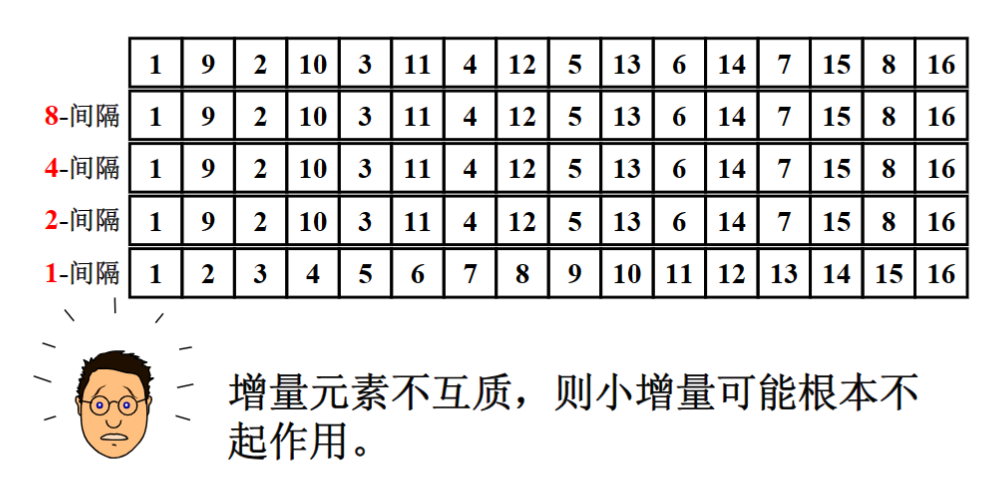
==所以，选择的增量元素是有说法的==

选择排序

选择排序（Selection Sort）是一种简单直观的排序算法，它的核心思想是每次从未排序的部分中选择最小（或最大）的元素，然后将其放到已排序部分的末尾，逐步构建有序序列。

void Seletion_Sort(ElementType A[], int N)
{
	for( i = 0; i < N ; i ++)
	{
		MinPosition = ScanForMin(A,i,N-1);
		//从A[i]到A[N-1]中找到最小元，赋值给MinPosition
		Swap(A[i],A[MinPosition]);
		//将未排序的最小元换到有序部分最后的位置
	}
}

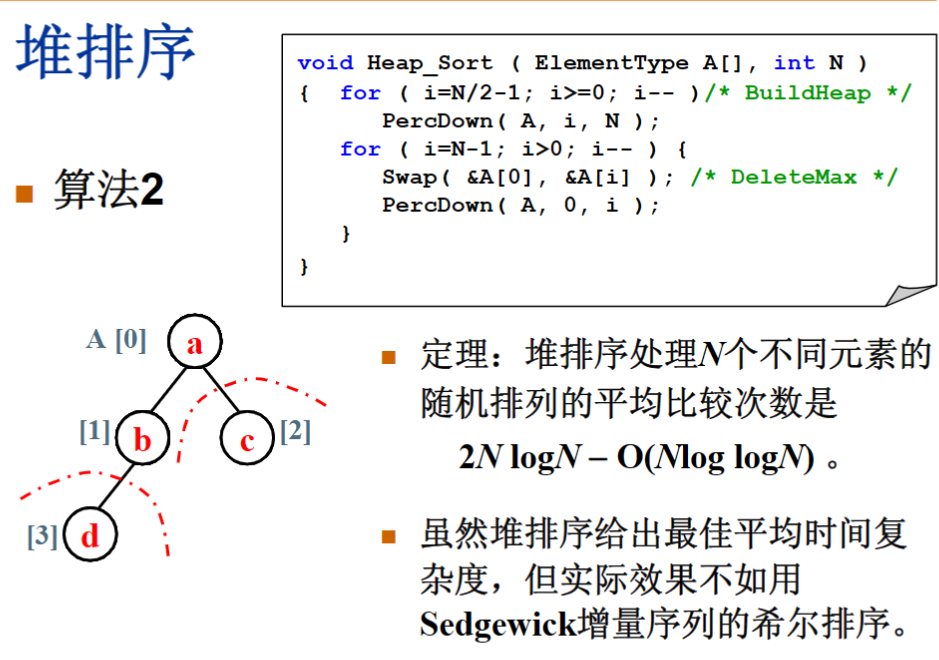
堆排序

堆排序（Heap Sort）是一种高效的不稳定排序算法，它基于二叉堆数据结构进行排序。堆排序的核心思想是将待排序的元素构建成一个二叉堆（最大堆或最小堆），然后逐步将堆顶元素与堆中的最后一个元素交换，然后将堆的大小减一，再对堆进行调整（维护堆的性质），重复这个过程直到堆为空，最终完成排序。

归并排序

归并排序（Merge Sort）是一种稳定的、分治法（Divide and Conquer）基础的排序算法，其核心思想是将待排序的数组划分为若干子数组，然后逐步将这些子数组合并成有序的数组。归并排序的过程可以描述为以下步骤：

我们定义三个元素，不断比肩a和b的数值，将小的给c，实现a，b两个有序序列的归并。